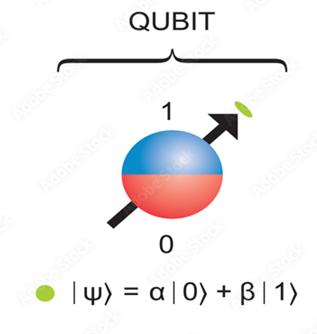
A qubit (short for quantum bit) is the fundamental unit of information in quantum computing, analogous to a classical bit in traditional computing.
While a classical bit can exist in only one of two states — 0 or 1 — a qubit can exist in a superposition of both states simultaneously. This property makes quantum computers vastly more powerful for certain computational tasks than their classical counterparts.

Key Characteristics of Qubits

1. Superposition

Superposition is the defining property that distinguishes qubits from classical bits. A qubit can represent both 0 and 1 at the same time, in different proportions, until it is measured. Mathematically, the state of a qubit can be written as: ∣ψ⟩=α∣0⟩+β∣1⟩

Here:

α and β are complex numbers known as probability amplitudes.
|α|^2 represents the probability of measuring the qubit in the |0⟩ state.
∣β∣^2 represents the probability of measuring the qubit in the |1⟩ state.
The normalization condition |α|^2 + |β|^2 = 1 must always hold true.

Superposition enables quantum computers to process multiple possibilities simultaneously, leading to parallel computation capabilities that classical systems cannot match.

2. Entanglement

Another remarkable property of qubits is entanglement. When two or more qubits become entangled, the state of one qubit becomes dependent on the state of another, regardless of the physical distance between them.

This phenomenon, described by Einstein as “spooky action at a distance,” allows for correlated outcomes — measuring one entangled qubit instantly determines the state of the other.
Entanglement is crucial for many quantum computing operations, including quantum teleportation, error correction, and secure communication.

3. Measurement

Measurement is a unique process in quantum mechanics. When a qubit is measured, it collapses from its superposition into one of its basis states — either |0⟩ or |1⟩.

This collapse is probabilistic, not deterministic:

The result depends on the probability amplitudes α and β.
Repeated measurements of identically prepared qubits yield statistical distributions rather than fixed outcomes.

Measurement, therefore, not only retrieves information but also destroys the superposition, marking the transition from the quantum to the classical world.

Types of Particles Used to Build Qubits

Qubits can be physically realized using a variety of quantum systems, each with unique properties and challenges.
Some commonly used physical implementations include:

Superconducting circuits (used by IBM and Google)
Trapped ions (used by IonQ and Honeywell)
Photons (used in optical quantum computing)
Spin qubits (based on electron or nuclear spins)
Neutral atoms and Rydberg atoms (emerging platforms for scalable quantum arrays)

(Source: Quantum Computing Hardware – An Introduction, YouTube)

How Different Types of Particles Are Used to Build Qubits

Quantum computers can be built using a variety of physical systems that exhibit quantum mechanical behavior — such as superposition and entanglement. These systems use different types of particles (electrons, photons, ions, atoms, etc.) or artificial quantum circuits to encode and manipulate information as qubits. Each qubit technology has its own strengths, weaknesses, and technical challenges, depending on how easily it can be controlled, how long it remains stable (coherence time), and how it interacts with other qubits.

Let’s examine the major types of particles and systems used to realize qubits.

1. Superconducting Qubits

Principle : Superconducting qubits are built from tiny superconducting circuits that behave like artificial atoms. They use the flow of Cooper pairs (paired electrons) in a superconducting loop to represent quantum states.

The two energy levels of the circuit correspond to the qubit states |0⟩ and |1⟩.

Particles Used

Electrons (as Cooper pairs in superconducting loops).

Examples

IBM, Google, and Rigetti use superconducting qubits.
Google’s Sycamore and IBM’s Eagle processors are based on this technology.

Advantages

Easily fabricated using microchip technology.
Fast gate operations (nanoseconds).
Integrates well with classical electronics.

Challenges

Requires ultra-low temperatures (near 15 millikelvin).
Sensitive to noise and decoherence.
Difficult to scale while maintaining qubit fidelity.

2. Trapped Ion Qubits

Principle

Trapped ion qubits use charged atomic particles (ions) suspended in an electromagnetic trap.
Quantum states are represented by different electronic or hyperfine energy levels of the ion.

Laser beams are used to manipulate and entangle ions by changing their energy levels or collective motion.

Particles Used

Ions (typically Calcium⁺, Ytterbium⁺, or Barium⁺).

Examples

Used by IonQ, Honeywell (Quantinuum), and several academic research groups.

Advantages

Extremely long coherence times (seconds to minutes).
High gate fidelity and precise control.
Operates at room or moderate vacuum conditions.

Challenges

Slower gate operations compared to superconducting qubits.
Scaling to large numbers of qubits is complex (requires multiple traps and optical connections).

3. Photonic Qubits

Principle

Photonic qubits use the quantum states of light particles (photons) to encode information.
The polarization, phase, or path of a photon can represent the |0⟩ and |1⟩ states.

Because photons travel at the speed of light and interact weakly with their environment, they are ideal for quantum communication and networking.

Particles Used

Photons (light particles).

Examples

Used in Xanadu’s Strawberry Fields platform.
Also employed in quantum key distribution (QKD) and optical quantum computing systems.

Advantages

Excellent for long-distance communication (low decoherence).
Can operate at room temperature.
Integrates with existing optical fiber networks.

Challenges

Weak photon–photon interactions make two-qubit gates difficult.
Requires highly efficient photon sources and detectors.

4. Spin Qubits

Principle

Spin qubits use the spin of particles — such as electrons or atomic nuclei — to represent quantum states.
A spin can point “up” (|0⟩) or “down” (|1⟩), or exist in a superposition of both.

They are controlled using microwave or magnetic fields that manipulate the spin direction.

Particles Used

Electrons (in quantum dots).
Nuclei (in nuclear magnetic resonance or donor atoms).

Examples

Used by Intel, Silicon Quantum Computing, and UNSW researchers (Australia).
Systems based on silicon quantum dots and phosphorus donor atoms.

Advantages

Long coherence times in pure materials (e.g., silicon).
Compatible with existing semiconductor manufacturing.
Energy-efficient and compact.

Challenges

Complex fabrication at the atomic scale.
Requires precise control over spin interactions.
Scaling beyond a few qubits remains difficult.

5. Neutral Atom and Rydberg Qubits

Principle

Neutral atoms (not charged) are cooled to near absolute zero and trapped using optical tweezers — tightly focused laser beams. Their quantum states are controlled using laser pulses.
When excited to Rydberg states (high-energy configurations), atoms exhibit strong interactions suitable for entangling operations.

Particles Used

Neutral atoms (e.g., Rubidium or Cesium).
Rydberg atoms (excited-state atoms with exaggerated electromagnetic properties).

Examples

Used by Atom Computing, QuEra, and Pasqal.
In 2023, TU Darmstadt demonstrated a 1,305-qubit Rydberg atom array — one of the largest ever.

Advantages

Highly scalable (thousands of atoms can be trapped in optical lattices).
Long coherence times.
Flexible and reconfigurable atomic arrays.

Challenges

Requires ultra-cold temperatures and high-precision laser control.
Readout and error correction are still developing.

6. Topological Qubits (Emerging Concept)

Principle

Topological qubits are theoretical and experimental constructs that encode quantum information in non-local properties of quasiparticles known as Majorana fermions.
These states are resistant to local noise, potentially making them intrinsically error-tolerant.

Particles Used

Quasiparticles (Majorana zero modes).

Examples

Being explored by Microsoft’s Quantum Lab and research groups using semiconductor–superconductor nanowires.

Advantages

Naturally robust against decoherence.
Potential for fault-tolerant quantum computation.

Challenges

Majorana fermions have not yet been conclusively observed.
Extremely difficult to engineer and control experimentally.

Basic Requirements of Quantum Hardware

Quantum hardware forms the physical foundation of a quantum computer — it is the system where qubits are created, manipulated, and measured.
Building reliable quantum hardware is extremely challenging because quantum systems are fragile and highly sensitive to their environment.
To perform meaningful quantum computations, any quantum hardware platform must meet several essential scientific and engineering requirements.

These requirements are often described in terms of the DiVincenzo criteria, proposed by physicist David P. DiVincenzo, which outline the basic physical principles needed to build a universal quantum computer.

Let’s explore these fundamental requirements.

1. Well-Defined and Scalable Qubits

Requirement:

The hardware must provide well-defined quantum states that can represent |0⟩ and |1⟩, as well as any superposition of these states.

Each qubit must be:

Isolated enough from the environment to maintain quantum coherence.
Distinct and controllable, allowing clear identification and addressing of each qubit.

Explanation:

The quantum bit must have two energy levels that act as computational states. These can be realized using:

Superconducting circuits,
Trapped ions,
Photons,
Electron or nuclear spins, or
Neutral atoms.

Moreover, the hardware should allow scalability — meaning that it can support hundreds or thousands of qubits without loss of performance or control.
Scalability is critical for building practical quantum processors capable of solving complex problems.

2. Initialization – The Ability to Set Qubits to a Known State

Requirement:

Quantum computations must start from a known, reproducible initial state, typically |0⟩ for all qubits.

Explanation:

Without reliable initialization, computations would produce random and unreliable results.
Quantum hardware must therefore include mechanisms to:

Cool qubits to their ground state (as in superconducting systems), or
Use optical pumping or laser cooling (as in trapped ion or neutral atom systems).

A well-defined starting state ensures predictability and reproducibility — key for both computation and error correction.

3. Long Coherence Time

Requirement:

Qubits must maintain their quantum coherence long enough to perform calculations.
Coherence refers to the ability of a qubit to remain in superposition and entanglement without interference from its surroundings.

Explanation:

Quantum systems are extremely sensitive to:

Temperature fluctuations,
Electromagnetic noise,
Vibrations, and
Interactions with other particles.

If a qubit loses coherence too quickly (a process known as decoherence), its quantum state collapses before computations are complete.
To be useful, coherence times must be much longer than gate operation times, allowing many quantum operations before errors accumulate.

Typical coherence times:

Superconducting qubits: microseconds to milliseconds.
Trapped ions: seconds to minutes.
Photonic qubits: effectively infinite during transmission (no decoherence in vacuum).

4. Quantum Gate Operations – Controlled Manipulation

Requirement:

The hardware must support a universal set of quantum gates, allowing precise control over qubit states and entanglement.

Explanation:

Quantum gates are reversible unitary transformations that rotate qubits on the Bloch sphere.
Hardware must enable:

Single-qubit gates (e.g., X, Y, Z, H) for rotations.
Two-qubit gates (e.g., CNOT, CZ) for entanglement.

High-quality quantum gates require:

Precise control pulses (microwave, laser, or magnetic).
Low error rates (below 0.1% for fault-tolerant thresholds).

Reliable gate operations are the “instruction set” of a quantum processor — they determine how accurately algorithms can be executed.

5. Qubit Connectivity and Entanglement

Requirement:

Qubits must be able to interact with each other to form entangled states.

Explanation:

Entanglement is essential for quantum computation — it allows qubits to share information and perform coordinated operations.
The hardware architecture must support:

Direct coupling between neighboring qubits (superconducting circuits, spin arrays), or
Mediated entanglement via photons or shared motion (in trapped ions).

The connectivity topology — how qubits are linked — determines algorithm efficiency and gate complexity.
Higher connectivity simplifies computation but is harder to maintain physically.

6. Reliable Measurement Capability

Requirement:

The hardware must provide a way to measure qubits accurately to determine computation outcomes.

Explanation:

Measurement collapses a qubit’s state into |0⟩ or |1⟩, producing classical information.
Hardware should ensure:

High readout fidelity (accuracy above 99%).
Fast, nondestructive measurement so multiple readouts can be taken if needed.

Different technologies use different measurement techniques:

Superconducting qubits use microwave resonators.
Trapped ions use fluorescence detection.
Photonic systems detect light polarization or arrival time.

Reliable measurement closes the computation loop and verifies results.

7. Error Correction and Fault Tolerance

Requirement:

Since quantum systems are error-prone, the hardware must support quantum error correction (QEC) mechanisms.

Explanation:

Quantum error correction encodes one logical qubit into many physical qubits, allowing detection and correction of errors without destroying quantum information.
This requires:

Extra qubits for redundancy.
Frequent error-syndrome measurements.
Fast feedback and control systems.

Example:
In 1998, researchers demonstrated the first quantum error correction using 9 physical qubits to encode a single logical qubit — a foundational milestone in quantum hardware development.

Fault-tolerant quantum hardware must have low gate error rates and sufficient qubit coherence to implement these complex correction protocols.

8. Scalability and Integration

Requirement:

Quantum hardware must be designed to scale up from a few qubits to thousands or millions while maintaining coherence and control.

Explanation:

Scaling requires:

Compact and uniform qubit architectures.
Efficient cryogenic systems or optical setups.
Integration with classical control electronics.

Large-scale integration challenges include:

Managing cross-talk between qubits.
Synchronizing control signals for hundreds of operations.
Implementing quantum interconnects to link multiple processors.

9. Environmental Isolation

Requirement:

Quantum systems must be well isolated from external disturbances to preserve quantum behavior.

Explanation:

Isolation techniques vary depending on the hardware type:

Superconducting qubits: operate in dilution refrigerators at ~15 millikelvin.
Ion and atom qubits: trapped in ultra-high vacuum chambers using lasers and magnetic fields.
Photonic qubits: transmitted in optical fibers or vacuum paths to minimize scattering and loss.

Isolation protects qubits from decoherence and thermal noise, which are the main enemies of quantum computation.

10. Classical Control and Readout Systems

Requirement:

Quantum hardware requires classical electronic systems for control, synchronization, and data processing.

Explanation:

Even though quantum operations are performed on qubits, they are initiated and read by classical electronics.
These include:

Microwave and laser control hardware.
Timing and pulse-shaping electronics.
Fast data acquisition systems for measurement readouts.

Integration between quantum and classical layers is vital for real-time feedback, error correction, and hybrid quantum-classical computation.

Summary Table: Core Hardware Requirements

Requirement	Purpose	Example Implementation
Well-defined qubits	Represent	0⟩,
Initialization	Start from known state	Laser cooling, ground-state preparation
Long coherence	Preserve quantum information	Cryogenic isolation, vacuum traps
Quantum gates	Manipulate qubits	Microwave or laser pulses
Entanglement	Enable multi-qubit operations	Coupled qubit networks
Measurement	Extract classical output	Optical detection, resonators
Error correction	Mitigate decoherence and noise	Logical qubits, redundancy
Scalability	Build large processors	Modular and integrated designs
Isolation	Reduce noise interference	Cryogenics, vacuum chambers
Classical control	Interface between user and hardware	Electronics, lasers, feedback systems

Quantum Computing Hardware: Key Milestones

The progress in qubit technology can be tracked through key milestones achieved by major research organizations and companies.

Year	Qubit Count	Milestone
1998	9	First demonstration of quantum error correction using 9 physical qubits to encode 1 logical qubit.
2016	5	IBM introduces 5-qubit processors: IBM Q 5 Tenerife and IBM Q 5 Yorktown.
2017	14	IBM launches the 14-qubit IBM Q 14 Melbourne processor.
	16	IBM Q 16 Rüschlikon introduced.
	17	IBM Q 17 processor unveiled.
	20	IBM Q 20 Tokyo released.
2018	20	IBM Q 20 Austin processor released.
	50	IBM introduces the 50-qubit IBM Q 50 Prototype.
2019	53	IBM launches the IBM Q 53 processor.
	53	Google claims quantum supremacy with its 53-qubit Sycamore processor.
2020	27	IBM achieves Quantum Volume 64 using a 27-qubit processor.
2021	127	IBM releases the Quantum Eagle 127-qubit processor.
2022	433	IBM unveils the Quantum Osprey processor.
2023	1,121	IBM presents the Quantum Condor 1,121-qubit processor.
	1,305	TU Darmstadt demonstrates a 1,305-qubit array based on optical tweezers.
	1,180	Atom Computing announces a 1,180-qubit array using Rydberg atoms.
2024	Up to 8 (fused states)	Researchers fuse small quantum states into larger states containing up to eight qubits.

These milestones reflect the rapid scaling of qubit technology and the steady progress toward more stable, error-tolerant quantum systems.

Challenges and Considerations

Although qubits offer immense computational potential, building practical quantum computers remains one of science’s greatest challenges. Three major issues dominate current research:

1. Decoherence

Quantum systems are highly sensitive to their environment. External interactions—such as temperature changes, vibrations, and electromagnetic fields—can cause a qubit to lose its quantum state, a process known as decoherence. Maintaining coherence is essential for performing reliable computations.

2. Error Correction

Unlike classical bits, qubits are prone to errors due to decoherence and noise. Quantum error correction techniques are being developed to protect quantum information by encoding a logical qubit using multiple physical qubits. For instance, the first demonstration of quantum error correction in 1998 used 9 physical qubits to encode 1 logical qubit.

3. Scalability

Building large-scale quantum computers involves balancing:

Qubit count (to increase computational power),
Connectivity (how qubits interact), and
Fidelity (how accurately they perform operations).

As systems scale beyond hundreds or thousands of qubits, managing noise, coherence time, and control precision becomes increasingly difficult. Researchers continue to explore new materials, architectures, and algorithms to overcome these limitations.