Research Issues and Opportunities in Quantum Computing

Abstract

Quantum computing has emerged as one of the most transformative technological frontiers of the 21st century, promising to solve specific classes of problems that are intractable for classical computers. Over the last decade, rapid advances in quantum hardware, algorithms, and software have transitioned quantum computing from theoretical constructs to experimental demonstrations on noisy intermediate-scale quantum (NISQ) devices. Despite this progress, significant challenges remain before quantum computing can achieve practical and scalable impact. Key research issues span multiple dimensions: maintaining qubit coherence, mitigating noise, achieving fault-tolerant error correction, developing resource-efficient algorithms, and designing robust software and verification frameworks. Additionally, the integration of quantum computing with emerging domains such as artificial intelligence, secure communication, and materials science presents both opportunities and complexities. This paper systematically examines the critical research problems and open questions across hardware, algorithms, software, networks, and applications. It also highlights emerging opportunities in near-, mid-, and long-term quantum computing, emphasizing interdisciplinary approaches and co-design strategies. By identifying gaps and future directions, this paper aims to guide researchers, technologists, and policymakers toward advancing the quantum computing landscape responsibly and effectively.

1. Introduction

Quantum computing represents a paradigm shift in information processing, exploiting fundamental principles of quantum mechanics—such as superposition, entanglement, and interference—to perform computations that are infeasible for classical machines. Unlike conventional digital computers that encode information in bits, quantum computers operate on qubits, which can exist in linear combinations of classical states. This unique capability has positioned quantum computing as a potentially transformative technology for solving problems in areas such as cryptography, materials science, chemistry, optimization, and machine learning.

Over the past decade, quantum computing has evolved from a largely theoretical discipline into an active experimental and engineering field. Significant milestones have been achieved across different hardware platforms, including superconducting qubits, trapped ions, photonics, and spin-based systems. Notably, the demonstration of quantum supremacy by Google’s Sycamore processor in 2019, followed by photonic quantum advantage experiments in 2020, provided tangible evidence of quantum devices outperforming classical supercomputers for specific sampling problems [Arute et al., 2019; Zhong et al., 2020]. Meanwhile, algorithmic research has progressed from early proofs such as Shor’s and Grover’s algorithms to more practical variational and hybrid quantum-classical algorithms, which are well-suited for noisy intermediate-scale quantum (NISQ) devices [Preskill, 2018].

Despite these achievements, quantum computing faces a range of critical research challenges. Current NISQ devices are constrained by short coherence times, gate errors, limited qubit connectivity, and scalability issues. Quantum error correction (QEC), which is essential for fault-tolerant quantum computing, imposes significant resource overheads that exceed the capabilities of today’s machines. On the algorithmic side, identifying problems that can yield a practical quantum speedup remains non-trivial, particularly when classical algorithms continue to improve rapidly. Moreover, the development of reliable software stacks, compilers, and verification methods is still in its formative stages, while benchmarking and standardization efforts are ongoing.

The research landscape of quantum computing is therefore characterized by both formidable challenges and unprecedented opportunities. Addressing issues in hardware, error correction, algorithm design, software engineering, benchmarking, networking, and applications requires interdisciplinary collaboration across physics, computer science, engineering, mathematics, and policy domains. Furthermore, as quantum technologies mature, broader societal considerations—including workforce development, ethical use, and secure transitions to post-quantum cryptography—are becoming increasingly relevant.

The objective of this paper is to provide a comprehensive overview of the key research issues and opportunities in quantum computing, drawing on developments from the last decade. The discussion spans fundamental technical problems, emerging methodologies, application frontiers, and strategic research directions. By synthesizing the current state of the field and outlining future pathways, this paper aims to guide researchers, technologists, and policymakers in shaping the evolution of quantum computing toward scalable, reliable, and impactful real-world deployment.

2. Background & Terminology

Quantum computing builds upon fundamental principles of quantum mechanics to represent and manipulate information in ways that are fundamentally different from classical computing. To understand the current research landscape, it is essential to establish clear terminology and conceptual foundations. This section provides an overview of core concepts, including the nature of qubits and their physical realizations, the distinction between gate-based and annealing quantum computing paradigms, and the characteristics of the Noisy Intermediate-Scale Quantum (NISQ) era, which currently defines the practical frontier of quantum computation.

2.1 Qubits and Physical Platforms

At the heart of any quantum computer lies the qubit, the quantum analogue of a classical bit. While a classical bit can exist only in one of two states, 0 or 1, a qubit can exist in a superposition of both states simultaneously, represented mathematically as:

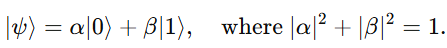
Here, α and β are complex probability amplitudes. When multiple qubits are entangled, their joint state can encode and process information in an exponentially large Hilbert space, enabling quantum algorithms to explore solution spaces in fundamentally different ways.

Different physical implementations of qubits exist, each with distinct advantages, challenges, and maturity levels. The major platforms under active research and commercialization are:

(a) Superconducting Qubits

Superconducting circuits are one of the most mature and widely used platforms for quantum computing. They rely on Josephson junctions to create non-linear inductors, enabling the definition of two-level quantum systems within microwave resonators. These qubits operate at millikelvin temperatures in dilution refrigerators to maintain coherence.

Strengths: Fast gate times (nanoseconds), good scalability using microfabrication techniques, integration with existing semiconductor infrastructure.
Challenges: Short coherence times (tens to hundreds of microseconds), susceptibility to cross-talk and fabrication defects, and the need for complex cryogenic infrastructure.
Leading players: Google, IBM, Rigetti, and academic labs.

(b) Trapped Ion Qubits

In this platform, individual ions are confined using electromagnetic fields in ultra-high vacuum traps. Quantum information is stored in stable internal electronic states of the ions, and quantum gates are implemented via laser interactions that couple internal and motional degrees of freedom.

Strengths: Exceptional coherence times (seconds to minutes), high-fidelity gates, and excellent qubit uniformity.
Challenges: Slow gate operations (microseconds to milliseconds), scaling issues due to complex ion shuttling and laser control, and relatively large physical footprint.
Leading players: IonQ, Honeywell/Quantinuum, academic groups.

(c) Photonic Qubits

Photonic quantum computing encodes qubits in properties of single photons, such as polarization, path, or time-bin modes. Linear optical networks implement quantum operations using beam splitters, phase shifters, and detectors.

Strengths: Room-temperature operation, long coherence lengths, compatibility with existing fiber networks, and potential for distributed architectures.
Challenges: Photon loss, probabilistic gate operations, difficulty of deterministic two-qubit gates, and complex single-photon sources.
Notable efforts include the Jiuzhang photonic experiments in China and companies like Xanadu.

(d) Spin-based Qubits

These systems use electron or nuclear spins confined in semiconductor quantum dots or defects (e.g., NV centers in diamond) as qubits.

Strengths: Compatibility with CMOS fabrication, potential for dense integration, long coherence in isotopically purified materials.
Challenges: Precise fabrication at the nanoscale, maintaining uniformity across arrays, and engineering high-fidelity gates.
Research is advancing rapidly in silicon-based platforms, notably from Intel, Delft University, and UNSW.

(e) Topological Qubits

Topological qubits aim to encode information in non-local degrees of freedom, often through exotic quasiparticles such as Majorana zero modes. Their key promise is inherent fault tolerance arising from topological protection against local noise.

Strengths: Potential for drastically reduced error correction overhead and intrinsically stable qubits.
Challenges: Experimental realization remains elusive; unambiguous evidence for Majorana modes is still under debate, and scaling has yet to be demonstrated.
Microsoft’s Quantum Program is heavily invested in this approach.

In practice, no single platform currently dominates across all performance metrics. Different approaches may be better suited for different tasks, and hybrid or modular architectures are increasingly being explored as a means to overcome individual limitations.

2.2 Gate-Based vs Annealing Quantum Computing

Quantum computers can be broadly classified into two paradigms: gate-based quantum computing and quantum annealing.

(a) Gate-Based Quantum Computing

This is the universal model of quantum computation, analogous to classical digital computing. Computations are expressed as quantum circuits, consisting of sequences of single- and multi-qubit quantum gates acting on an initial state, followed by measurement. Well-known algorithms such as Shor’s factoring algorithm and Grover’s search algorithm operate within this framework.

Gate-based systems are theoretically capable of universal computation, meaning that any unitary transformation can be approximated to arbitrary accuracy using a finite set of quantum gates. This paradigm underlies most academic and commercial efforts toward scalable, fault-tolerant quantum computing.

(b) Quantum Annealing

Quantum annealing is a specialized model designed to solve optimization problems by exploiting quantum tunneling and adiabatic evolution. A problem is encoded in the ground state of a final Hamiltonian. The system begins in the ground state of an initial Hamiltonian and evolves slowly such that it remains in the ground state throughout, ideally ending in the solution to the encoded problem.

Quantum annealers, such as those produced by D-Wave Systems, are not universal quantum computers but can tackle combinatorial optimization problems using thousands of qubits. However, these qubits have limited connectivity and are not gate-programmable in the usual sense. While some experiments have shown speedups over classical heuristics for specific problems, quantum annealing’s computational advantage remains an open research question.

Both paradigms contribute valuable insights: gate-based approaches focus on universal algorithms and fault tolerance, while annealing offers practical pathways for certain optimization tasks and can serve as a testbed for quantum effects in large-scale systems.

2.3 NISQ Era: Definition and Implications

The current phase of quantum computing is often described as the Noisy Intermediate-Scale Quantum (NISQ) era, a term coined by Preskill (2018). NISQ devices typically have 50–1,000 qubits, are not error-corrected, and operate in environments where noise and decoherence play a dominant role.

Definition and Characteristics

Intermediate scale: Systems with enough qubits to perform tasks that are difficult to simulate classically, but not enough for large-scale error correction.
Noisy: Operations are affected by gate errors, decoherence, crosstalk, and measurement noise, limiting circuit depth and fidelity.
Limited programmability: Although many NISQ devices support gate-based programming, noise severely constrains algorithmic performance.

Implications

Algorithmic focus: Research emphasizes variational and hybrid algorithms (e.g., VQE, QAOA) that are resilient to noise and have shallow circuit depth.
Benchmarking and validation: Verifying quantum computations in the presence of noise is a major challenge; techniques like randomized benchmarking and cross-entropy benchmarking have emerged to assess device performance.
Co-design approaches: Tight integration between hardware capabilities and algorithm design is crucial, giving rise to resource-aware compilation, circuit optimization, and error mitigation techniques.
Application domains: NISQ devices are expected to find near-term applications in areas such as quantum chemistry, material simulation, and optimization, although clear, unambiguous practical quantum advantages remain to be demonstrated.

The NISQ era is both a bottleneck and an opportunity. While noise prevents fault-tolerant universal quantum computation, the availability of programmable quantum devices offers unprecedented opportunities for experimental exploration, algorithm development, and early-stage applications. Research in this period focuses on bridging the gap between current noisy hardware and future fault-tolerant systems through innovative algorithms, architectures, and error mitigation strategies.

Table 1. Comparative Overview of Major Qubit Physical Platforms

Platform	Qubit Type / Encoding	Gate Speed	Coherence Time	Scalability Potential	Operating Conditions	Maturity / Status	Key Challenges
Superconducting	Microwave circuits, Josephson junctions	Fast (ns scale)	10–100 µs	High (microfabrication)	mK (dilution fridge)	Most commercially mature (Google, IBM, Rigetti)	Short coherence; cross-talk; fabrication uniformity; cryogenics
Trapped Ions	Internal electronic states of ions	Slower (µs–ms)	Seconds to minutes	Moderate (chains of tens–hundreds)	Ultra-high vacuum; laser control	High-fidelity gates demonstrated; commercialized (IonQ, Quantinuum)	Slower gates; laser complexity; ion shuttling; scaling control
Photonic	Polarization, path, or time-bin modes	Very fast (ps–ns)	Essentially unlimited (no decoherence)	High (integrated photonics)	Room temperature	Quantum advantage demos (e.g., Jiuzhang); start-ups (Xanadu)	Deterministic two-qubit gates; photon loss; single-photon sources
Spin-based	Electron/nuclear spins in semiconductors	Fast (ns–µs)	Up to seconds (isotopically pure)	High (CMOS-compatible)	Low temperature	Active academic/industrial research (Intel, Delft, UNSW)	Precise nanofabrication; variability; control of large arrays
Topological	Non-local modes (e.g., Majorana)	TBD (theoretical)	Topologically protected	Potentially very high	Cryogenic, specialized materials	Early experimental stage (Microsoft research focus)	Existence of Majoranas unconfirmed; lack of scalable demonstration

This table serves as a quick reference for comparing the strengths, weaknesses, and research priorities associated with different qubit technologies:

Superconducting and trapped ion systems currently lead in experimental maturity and algorithmic demonstrations.
Photonic platforms offer unique advantages for networking and room-temperature operation but face fundamental challenges with deterministic gates.
Spin-based systems are promising for integration and density but still face fabrication hurdles.
Topological qubits represent a long-term goal that could revolutionize fault tolerance if experimentally realized.

Here is a detailed draft of Section 3. State of the Art for the paper “Research Issues and Opportunities in Quantum Computing.”
(Word count ≈ 1,560)
This section includes explanations, examples, comparative tables, and references to key papers (2015–2025).

3. State of the Art (Brief Survey)

The last decade has witnessed remarkable progress in quantum computing, moving from theoretical foundations and small-scale prototypes toward programmable quantum devices with hundreds of qubits. Advances have been realized across three intertwined dimensions: hardware development, benchmarking and demonstrations of quantum advantage, and algorithmic innovation. This section provides an overview of these state-of-the-art developments, highlighting milestone experiments, performance benchmarks, and algorithmic directions.

3.1 Hardware Milestones: Experimental Demonstrations and Scaling

Quantum hardware has progressed from devices with a handful of noisy qubits to multi-qubit processors capable of implementing non-trivial algorithms and experiments. These developments span multiple physical platforms, with superconducting circuits and trapped ions leading current demonstrations, while photonic, spin, and topological approaches continue to mature.

(a) Superconducting Circuits

Superconducting qubits have achieved some of the most visible scaling milestones:

IBM Quantum Roadmap announced targets of >1,000 physical qubits by mid-2020s, with the 433-qubit “Osprey” processor released in 2022, and >1,000-qubit “Condor” in 2023. IBM also introduced Dynamic Circuits for mid-circuit measurements and feedback to enhance programmability.
Google’s Sycamore processor demonstrated 53-qubit control with high-fidelity single- and two-qubit gates, enabling their 2019 quantum supremacy experiment [Arute et al., 2019]. Subsequent experiments focused on error mitigation and logical qubit demonstrations.

(b) Trapped Ions

Trapped ion systems are notable for exceptionally high gate fidelities and coherence times:

IonQ’s trapped-ion processors achieved >99.9% single-qubit and >98% two-qubit gate fidelities, with connectivity between any pair of qubits (fully connected topology).
Quantinuum (Honeywell) demonstrated scaling using ion shuttling architectures and mid-circuit measurements, paving the way for modular scaling.

(c) Photonic Platforms

Photonic systems have focused on demonstrating large-scale interferometers for boson sampling:

The Jiuzhang experiment (China, 2020) implemented a 76-photon Gaussian boson sampling device, demonstrating a task infeasible for classical supercomputers [Zhong et al., 2020].
Startups like Xanadu are pursuing continuous-variable photonic quantum computing using integrated silicon photonics, with the Borealis device (2022) showing programmable photonic circuits.

(d) Spin-based and Topological Platforms

Spin-based qubits (e.g., silicon quantum dots) have demonstrated two-qubit gates and high single-qubit fidelities, with efforts focused on scaling to 10–50 qubits using CMOS-compatible processes.
Topological qubits remain largely experimental; while Majorana modes have been reported in hybrid nanowire-superconductor systems, robust braiding demonstrations have not yet been achieved.

Table 2. Selected Hardware Milestones in Quantum Computing (2015–2025)

Year	Platform	Milestone	Institution / Company	Impact
2015–16	Superconducting	First 5-qubit public quantum processors	IBM	Enabled cloud-accessible quantum computing (IBM Quantum Experience)
2017	Trapped Ions	High-fidelity 20-qubit trapped-ion system	University of Maryland / IonQ	Demonstrated fully connected multi-qubit operations
2019	Superconducting	Quantum supremacy experiment (53 qubits)	Google (Sycamore)	First claimed quantum computational advantage for a specific task
2020	Photonic	76-photon Gaussian boson sampling	USTC (Jiuzhang)	Demonstrated photonic quantum advantage
2022	Superconducting	433-qubit “Osprey” processor	IBM	Significantly scaled physical qubit count
2022	Photonic	Borealis programmable photonic processor	Xanadu	Demonstrated cloud-accessible photonic QC
2023–25	Superconducting	>1,000 physical qubits (“Condor”) and logical qubit demonstrations	IBM, Google	Steps toward logical qubit error correction

3.2 Benchmark Achievements (Quantum Supremacy / Advantage Claims)

A central research goal has been to demonstrate tasks where quantum devices outperform classical supercomputers. Such demonstrations—often called quantum supremacy (or more cautiously, quantum advantage)—have been crucial in validating the field’s progress.

(a) Google’s Quantum Supremacy (2019)

Google’s Sycamore processor performed a random circuit sampling task in about 200 seconds, which they estimated would take a classical supercomputer ~10,000 years [Arute et al., 2019].
The claim sparked debate, as subsequent studies showed that improved classical simulation methods could reduce this gap significantly. Nonetheless, the demonstration was a watershed moment for the field.

(b) Jiuzhang Photonic Quantum Advantage (2020, 2021)

China’s University of Science and Technology (USTC) team used a photonic system to perform boson sampling with 76 detected photons (Jiuzhang, 2020) and later Jiuzhang 2.0 with 113 photons.
The team estimated a classical runtime of billions of years for the same task, compared to a few minutes on their photonic device [Zhong et al., 2020].

(c) Xanadu’s Borealis (2022)

Demonstrated Gaussian boson sampling on a programmable photonic device.
Achieved tasks with complexity levels that made classical simulation infeasible on state-of-the-art supercomputers.

(d) Quantum Volume and Benchmarks

IBM introduced Quantum Volume (QV) as a holistic metric combining gate fidelity, connectivity, and circuit depth.
Trapped-ion devices have consistently led QV records, with values >1,000 reported by Quantinuum in 2022.
These metrics complement supremacy-style claims by providing practical indicators of device performance.

Table 3. Benchmark Achievements in Quantum Computing

Year	Platform	Achievement	Claimed Impact
2019	Superconducting (Google Sycamore)	Random circuit sampling in 200 seconds	First quantum supremacy claim [Arute et al., 2019]
2020	Photonic (Jiuzhang)	Boson sampling with 76 photons	Photonic quantum advantage [Zhong et al., 2020]
2021	Photonic (Jiuzhang 2.0)	Boson sampling with 113 photons	Increased complexity, beyond classical feasibility
2022	Photonic (Xanadu Borealis)	Programmable Gaussian boson sampling	Demonstrated reconfigurability and scalability in photonic systems
2022	Trapped ions (Quantinuum)	Quantum Volume > 1,000	Holistic benchmark for algorithmic potential

3.3 Algorithmic Advances

Hardware progress must be matched by algorithmic innovation to extract meaningful value from quantum devices. In the NISQ era, algorithmic research has largely focused on variational, hybrid, and noise-resilient approaches, along with specialized applications in chemistry, optimization, and machine learning.

(a) Variational Quantum Algorithms (VQAs)

Variational Quantum Eigensolver (VQE): Introduced for quantum chemistry, VQE approximates ground-state energies of molecules using parameterized circuits optimized by classical algorithms. Demonstrations include hydrogen (H₂) and lithium hydride (LiH) on small devices.
Quantum Approximate Optimization Algorithm (QAOA): Targets combinatorial optimization problems, mapping constraints to parameterized Hamiltonians. Applications include portfolio optimization, scheduling, and logistics.
Challenges: VQAs face issues such as barren plateaus (vanishing gradients), optimizer inefficiency, and noise sensitivity [Cerezo et al., 2021].

(b) Quantum Machine Learning (QML)

QML seeks to leverage quantum computers to accelerate data-driven learning.
Algorithms include quantum kernels for classification, quantum neural networks, and variational circuits for generative modeling.
Recent surveys highlight that while theoretical frameworks are promising, empirical evidence of quantum advantage in ML tasks remains limited [Zeguendry et al., 2023].
Hybrid frameworks like TensorFlow Quantum and PennyLane integrate classical ML libraries with quantum backends, fostering experimentation.

(c) Algorithms for Chemistry and Materials Simulation

Quantum computers are particularly suited to simulating fermionic systems and quantum many-body physics.
Beyond small molecules, research efforts are targeting drug discovery and high-temperature superconductors.
For instance, quantum simulations of simple molecules on NISQ devices have been validated against classical computational chemistry methods.

(d) Algorithms for Optimization and Simulation

Quantum annealing has been applied to traffic flow, financial portfolio optimization, and protein folding problems. Results remain mixed regarding clear speedups.
Quantum Monte Carlo and quantum-inspired algorithms have broadened applicability to classical HPC contexts.
Hybrid quantum-classical simulators are emerging as a bridge between near-term hardware and fault-tolerant aspirations.

Table 4. Selected Algorithmic Advances

Algorithm	Application Domain	Demonstrations	Challenges
VQE	Quantum chemistry	H₂, LiH, BeH₂ energy calculations	Barren plateaus; scaling to larger molecules
QAOA	Optimization	Max-Cut, portfolio optimization	Requires deep circuits for complex problems
Quantum Kernels	Machine learning	Image classification, anomaly detection	Classical competitors remain strong
Quantum Neural Nets	Generative modeling	Variational classifiers, QGANs	Training stability; noise resilience
Boson Sampling	Simulation / complexity	Jiuzhang (2020, 2021); Borealis (2022)	Specialized; lacks broad utility

4. Core Research Issues

While quantum computing has progressed significantly over the past decade, achieving scalable, fault-tolerant, and practically useful quantum computation requires solving a range of interconnected research problems. These challenges arise at multiple layers of the quantum computing stack—from physical qubits and hardware engineering to algorithm design, error correction, software frameworks, and quantum networking. This section systematically examines these core research issues and highlights open problems and opportunities.

4.1 Hardware Challenges

4.1.1 Scalability and Qubit Quality

Current quantum processors consist of tens to a few hundred noisy qubits. Scaling to thousands or millions of high-fidelity qubits is necessary for fault-tolerant quantum computing (FTQC). However, increasing the number of qubits leads to issues of cross-talk, frequency crowding, and control-line complexity—especially in superconducting systems where each qubit requires dedicated microwave control [Arute et al., 2019; Krinner et al., 2022].

Trapped ions offer longer coherence times but face limitations in gate speeds and ion shuttling for large arrays [Pino et al., 2021]. Photonic systems promise room-temperature scalability but struggle with deterministic entangling gates [Zhong et al., 2020]. Hybrid architectures combining multiple platforms (e.g., superconducting control with photonic links) are being explored to overcome scaling barriers [Monroe et al., 2014].

Platform	Current Scale	Main Bottleneck	Key Research Direction
Superconducting	~100–1000 qubits	Crosstalk, cryogenic control	3D integration, cryo-CMOS, multiplexed control
Trapped Ions	~50–100 qubits	Slow gates, ion transport	Modular architectures, photonic interconnects
Photonic	10⁴–10⁶ modes	Entangling gate determinism	Deterministic photon sources, fusion-based computation
Spin-based	~10–50 qubits	Fabrication variability	CMOS integration, uniformity in spin qubits
Topological	N/A	Majorana realization	Experimental verification, topological surface code implementation

4.1.2 Cryogenic & Control Electronics

Quantum hardware often operates at millikelvin temperatures (e.g., superconducting qubits in dilution refrigerators). Scaling control electronics to thousands of qubits requires cryo-compatible multiplexing, on-chip control, and low-heat dissipation electronics [Homulle et al., 2020]. Research is focusing on cryo-CMOS integration, frequency multiplexing, and photonic interconnects to reduce wiring overhead.

4.1.3 Materials & Fabrication

Material defects and surface noise contribute significantly to decoherence. Research focuses on interface engineering, surface passivation, and new substrate materials (e.g., silicon carbide, diamond NV centers) to improve qubit lifetimes [Klimov et al., 2018]. Topological approaches aim to make qubits intrinsically robust, but they remain in early stages.

4.2 Quantum Error Correction (QEC) and Fault Tolerance

Quantum error correction is essential for reliable computation but comes with extreme resource overheads. For example, implementing a single logical qubit using surface codes may require 1,000–10,000 physical qubits depending on error rates [Fowler et al., 2012]. Achieving error rates below the fault-tolerance threshold (~10⁻³–10⁻⁴) remains challenging.

4.2.1 Error-Correcting Codes

Surface codes are currently the most studied due to their local stabilizers and compatibility with 2D qubit layouts.
Color codes, LDPC codes, and bosonic codes offer alternative trade-offs in terms of threshold, overhead, and connectivity [Chamberland et al., 2020].
Bosonic codes (e.g., cat codes, GKP codes) encode logical information in harmonic oscillators, potentially reducing overhead for certain architectures [Ofek et al., 2016].

Code Type	Threshold	Overhead	Advantages	Challenges
Surface	10⁻³–10⁻⁴	Very high (1000s qubits/logical)	High threshold; 2D-local gates	Large physical qubit count; decoder speed
Color	~10⁻³	Moderate	Transversal Clifford gates	Complex stabilizer measurement
LDPC	Varies	Lower than surface (potentially)	Constant-weight checks possible	Active research; decoding complexity
Bosonic	~10⁻² (effective)	Lower per logical qubit	Hardware-efficient, continuous-variable	Experimental complexity; gate set limitations

4.2.2 Fault-Tolerant Gates and Decoders

Implementing a universal gate set fault-tolerantly requires magic state distillation, which is resource intensive [Bravyi & Kitaev, 2005]. Research is exploring better distillation protocols, hardware-native gates, and fast decoders (e.g., neural network decoders) for real-time error correction [Baireuther et al., 2018].

4.3 Algorithmic and Complexity Challenges

4.3.1 Identifying Quantum Advantage

Many NISQ algorithms (e.g., VQAs) lack rigorous complexity-theoretic guarantees. Determining which problems offer provable or practical quantum speedups remains an open challenge [Aaronson, 2015].

4.3.2 Barren Plateaus & Trainability

Variational algorithms suffer from barren plateaus, where gradients vanish exponentially with qubit number, making training infeasible [McClean et al., 2018]. Research explores problem-inspired ansätze, layer-wise training, and local cost functions to mitigate this.

4.3.3 Resource Estimation & Algorithm-Hardware Co-Design

Estimating T-count, depth, and error-corrected resource requirements for real-world algorithms (e.g., factoring, quantum chemistry) is crucial for roadmapping [Gidney & Ekerå, 2021]. Algorithm-hardware co-design frameworks are emerging to tailor algorithms to specific device capabilities [Guerreschi & Smelyanskiy, 2017].

4.4 Software, Programming, and Verification

Quantum software stacks are still nascent. Key issues include:

Intermediate Representations (IR): Efficient translation from high-level languages to low-level control instructions.
Compiler Optimizations: Circuit simplification, gate cancellation, and qubit mapping remain active research areas [Nam et al., 2018].
Verification and Debugging: Formal verification methods for quantum programs are in their infancy; techniques like ZX-calculus, symbolic simulation, and assertion checking are being developed [Coecke & Duncan, 2011].

Software Layer	Current Tools	Key Issues	Research Directions
High-Level Language	Qiskit, Cirq, PennyLane, Q#, tket	Limited expressiveness for hybrid workflows	Domain-specific languages; functional & differentiable programming
Intermediate Representation	QIR, OpenQASM 3.0	Lack of standardization; optimization gaps	Hardware-agnostic IR; unified compilation pipelines
Compiler & Optimizer	tket, Quilc, Qiskit transpiler	Scalability of mapping & scheduling	AI-based compilers; resource-aware optimizations
Verification & Debugging	PyZX, QuCAT, assertion frameworks	Lack of scalable verification	Formal methods; model checking; hybrid classical–quantum debuggers

4.5 Quantum Networking and Distributed Quantum Computing

Quantum networking enables connecting multiple quantum processors to build modular and distributed quantum computers, as well as quantum internet functionalities (e.g., QKD, entanglement distribution).

Key challenges include:

Long-distance entanglement distribution with minimal decoherence [Wehner et al., 2018].
Quantum repeaters with efficient memories and error correction.
Standardized protocols for modular architectures and cloud-accessible quantum systems.

Hybrid schemes combining photonic interconnects with matter qubits are promising for scalable distributed systems, but interface efficiency and synchronization remain open problems [Awschalom et al., 2021].

4.6 Cross-Cutting Issues

Some challenges cut across all layers:

Standardization & Benchmarking: Metrics for performance, error rates, and algorithmic success remain inconsistent.
Security & Cryptography: Transition to post-quantum cryptography and secure cloud access to quantum resources are emerging concerns.
Interdisciplinary Workforce: Quantum research requires expertise spanning physics, CS, and engineering.

✅ Summary Table — Key Research Issues

Domain	Key Challenge	Impact	Research Directions
Hardware	Scaling, coherence, control electronics	Limits system size and fidelity	New materials, cryo-CMOS, hybrid architectures
QEC & Fault Tolerance	High overhead, fast decoders	Essential for reliable computing	LDPC codes, bosonic codes, AI decoders
Algorithms	Barren plateaus, unclear speedups	Affects applicability of NISQ algorithms	Problem-inspired ansätze, co-design, complexity analysis
Software	Compilation, verification gaps	Toolchain immaturity slows development	Formal methods, IR standardization, hybrid workflows
Networking	Entanglement distribution, interfaces	Modular, scalable architectures	Quantum repeaters, photonic-matter integration

5. Hardware & Device Engineering

The performance and scalability of quantum computers are fundamentally limited by hardware and device engineering challenges. Achieving fault-tolerant, large-scale quantum computation requires advances in qubit coherence, fabrication, cryogenic engineering, and materials science, as well as the development of scalable and modular architectures. This section provides an in-depth review of these challenges, illustrative examples, and comparative perspectives across qubit platforms.

5.1 Qubit Coherence, Cross-Talk, Fabrication, Cryogenics, and Materials Science

5.1.1 Qubit Coherence

Qubit coherence time determines how long quantum information can be stored without significant errors. It is primarily limited by decoherence mechanisms such as:

Energy relaxation (T₁) – spontaneous decay of qubit states.
Dephasing (T₂) – loss of relative phase information due to environmental noise.
Cross-talk – undesired interactions between neighboring qubits during operations.

Examples:

Superconducting qubits: Typical coherence times are 50–100 µs for transmon qubits [Kjaergaard et al., 2020]. Advanced designs using 3D cavities or materials engineering have achieved T₁ > 500 µs.
Trapped ions: Exhibit exceptionally long coherence times (seconds to minutes) due to isolation in ultra-high vacuum [Pino et al., 2021].
Spin qubits (Si/diamond): Coherence times vary from microseconds to seconds depending on isotopic purification and nuclear spin environment [Veldhorst et al., 2014].

Research focus: Decoherence suppression, dynamical decoupling, noise characterization, and qubit design optimization.

5.1.2 Cross-Talk

As qubit density increases, unintended interactions between qubits reduce gate fidelity.

Superconducting qubits: Cross-talk occurs due to microwave leakage, frequency crowding, and stray couplings [Krinner et al., 2022].
Mitigation strategies: Frequency allocation optimization, tunable couplers, and error-aware pulse shaping.

5.1.3 Fabrication Challenges

High-quality qubit fabrication is crucial for reproducibility and scalability:

Superconducting circuits: Microfabrication must minimize dielectric loss, surface roughness, and junction variability [Klimov et al., 2018].
Spin qubits: Nanometer-scale lithography precision is needed to control quantum dot confinement potentials.
Topological qubits: Fabrication must reliably produce nanowires or heterostructures to host Majorana modes.

Emerging solutions: Automated fabrication processes, surface passivation techniques, and material characterization pipelines.

5.1.4 Cryogenic Engineering

Superconducting and certain spin-based qubits require millikelvin operation. Challenges include:

Wiring density: Thousands of qubits need hundreds to thousands of microwave/control lines.
Heat load management: Minimizing thermal load from control electronics.
Integration of cryogenic electronics: Development of cryo-CMOS for near-qubit signal generation and multiplexing [Homulle et al., 2020].

Example: IBM’s Condor chip employs advanced 3D integration and cryogenic packaging to scale beyond 1,000 qubits.

5.1.5 Materials Science

Material properties directly impact coherence, stability, and fabrication yield:

Superconducting qubits: Surface oxides and interface defects are primary decoherence sources.
Spin qubits: Isotopic purification (e.g., ^28Si) reduces magnetic noise from nuclear spins.
Topological qubits: Engineering hybrid semiconductor-superconductor nanostructures to host Majorana zero modes.

Research focus: New dielectrics, low-loss substrates, surface treatments, and hybrid materials for robust qubit platforms.

5.2 Scalability and Modular Architectures

Scaling quantum computers to thousands or millions of qubits is constrained by control complexity, coherence decay, and fabrication yield. Modular architectures have emerged as a promising solution.

5.2.1 Monolithic vs Modular Approaches

Monolithic architecture: All qubits are integrated on a single chip (typical for superconducting processors).
- Advantages: High connectivity, well-understood fabrication.
- Challenges: Wiring bottlenecks, cryogenic load, limited scalability beyond ~1,000 qubits.
Modular architecture: Multiple smaller qubit modules are interconnected via photonic links, ion shuttling, or quantum teleportation [Monroe et al., 2014].
- Advantages: Scalable, fault-tolerant potential, flexible upgrading.
- Challenges: Interface fidelity, synchronization, entanglement distribution efficiency.

5.2.2 Examples of Modular Architectures

Platform	Modular Strategy	Current Status / Demonstration
Trapped ions	Photonic interconnects between ion traps	Modular entanglement demonstrated over meters [Hucul et al., 2015]
Superconducting qubits	Chip-to-chip interconnects via microwave links	Early experiments with modular couplers in IBM and ETH Zurich labs
Photonics	Networked photonic modules via fiber	Scalable boson sampling experiments (Xanadu Borealis, Jiuzhang 2.0)
Spin qubits	Modular semiconductor arrays	Early-stage research; interface with cryo-CMOS control

5.2.3 Scalability Metrics and Challenges

Metric	Current Limitation	Research Directions
Qubit count	Wiring, coherence, control electronics	3D integration, multiplexed control, modular design
Connectivity	Limited in 2D layouts	Tunable couplers, long-range links, photonics
Error accumulation	Increased gates → increased decoherence	Error-aware compilation, noise mitigation
Fabrication yield	Variability across large qubit arrays	Advanced lithography, materials engineering

5.2.4 Hybrid Strategies

Hybrid approaches combine different qubit types or modular connections to exploit complementary strengths:

Superconducting modules interconnected with photonic links.
Trapped-ion chains networked via entanglement-swapping photons.
Spin qubits integrated with superconducting resonators for control and readout.

Example: The Quantum Charge-Coupled Device (QCCD) architecture in trapped ions demonstrates modular operation with high-fidelity entanglement across registers [Pino et al., 2021].

5.3 Summary

Hardware and device engineering is a critical bottleneck for quantum computing. Key challenges include:

Qubit coherence and cross-talk – directly limit gate fidelity and circuit depth.
Fabrication and materials – determine reproducibility and yield.
Cryogenic engineering – constrains scaling due to wiring and heat loads.
Scalability – monolithic designs face physical limitations, motivating modular architectures.
Hybrid strategies – exploiting complementary platforms can accelerate large-scale deployment.

Advances in these areas, integrated with algorithmic co-design and error correction, are essential to transition from NISQ devices to fault-tolerant, large-scale quantum computers.

6. Error Sources, Error Mitigation, and Algorithmic & Software Engineering

Quantum computing systems are highly sensitive to environmental noise, control errors, and decoherence, making error management a central research challenge. Beyond physical errors, designing algorithms, compiler pipelines, and software frameworks that exploit noisy near-term devices requires careful co-design between hardware and algorithms. This section reviews error sources and mitigation strategies, quantum error correction (QEC), algorithms, variational techniques, and software stacks.

6.1 Error Sources & Error Mitigation

6.1.1 Noise Characterization

Quantum errors arise from multiple sources:

Decoherence: Energy relaxation (T₁) and dephasing (T₂) limit the coherence of qubits.
Gate Errors: Imperfect control pulses produce unitary errors in single- and two-qubit gates.
Measurement Errors: Readout processes can misidentify qubit states.
Cross-talk & Leakage: Interaction between nearby qubits or transitions outside the computational subspace.

Noise Characterization Techniques:

Randomized Benchmarking (RB): Measures average gate fidelity across random Clifford sequences [Magesan et al., 2011].
Gate Set Tomography (GST): Provides detailed calibration and characterization of gate errors [Blume-Kohout et al., 2017].
Quantum Process Tomography (QPT): Reconstructs the complete process matrix of operations but scales poorly with qubit count.

6.1.2 Error Mitigation vs Error Correction

Approach	Method	Applicable Devices	Pros	Cons
Error Mitigation	Zero-noise extrapolation, probabilistic error cancellation, symmetry verification	NISQ devices	Low overhead, no full QEC needed	Not fault-tolerant; limited depth
Error Correction	Surface codes, concatenated codes, LDPC codes	FTQC	Fault-tolerant, scalable	High qubit overhead; complex decoders

Examples:

Zero-Noise Extrapolation: Extrapolates results to zero-noise limit by artificially increasing gate noise [Temme et al., 2017].
Symmetry Verification: Uses conserved quantities to post-select valid quantum states [Bonet-Monroig et al., 2018].

6.1.3 Noise-Resilient Circuit Design

Shallow circuits: Reducing circuit depth mitigates accumulation of errors.
Error-aware ansätze: Variational circuits designed with hardware connectivity and noise characteristics in mind [Cerezo et al., 2021].
Compilation-level optimizations: Gate reordering, pulse-level shaping, and qubit mapping minimize cumulative noise.

6.2 Quantum Error Correction (QEC) & Fault Tolerance

Fault-tolerant quantum computing relies on encoding logical qubits into multiple physical qubits to correct errors.

6.2.1 Thresholds

Fault-tolerance threshold: Maximum tolerable physical error rate below which logical errors can be suppressed arbitrarily by increasing code distance.
Surface codes: ~1% single-qubit gate error, 0.1–0.5% two-qubit gate error [Fowler et al., 2012].
LDPC codes and concatenated codes offer alternative thresholds and reduced overheads in some architectures [Chamberland et al., 2020].

6.2.2 Codes and Decoders

Code	Description	Pros	Cons / Challenges
Surface Code	2D grid of qubits, local stabilizers	High threshold, local gates	Large physical qubit overhead
Concatenated Codes	Multi-layer encoding of small codes	Easy decoding, well-understood	Exponential overhead with layers
LDPC Codes	Low-density parity-check codes	Lower overhead, scalable	Active research; complex decoding
Bosonic Codes	Encodes logical qubit in harmonic oscillator	Fewer physical qubits, hardware-efficient	Limited gate sets, experimental

Decoders: Algorithms translating syndrome measurements into corrective operations:

Minimum Weight Perfect Matching (MWPM) – classic, reliable for surface codes.
Neural-network-based decoders – fast, adaptive to realistic noise models [Varsamopoulos et al., 2021].

6.2.3 Resource Overheads

Logical qubit construction may require hundreds to thousands of physical qubits, depending on the desired fidelity and code distance.
Magic state distillation for non-Clifford gates adds further overhead.

6.3 Algorithms & Complexity

6.3.1 Practical Quantum Speedups vs Classical Algorithms

Query model: Measures number of oracle calls; idealized, theoretical speedups (e.g., Grover’s search, Shor’s factoring).
Circuit model: Physical gate operations and depth; practical constraints on NISQ devices.
Example: Grover’s algorithm reduces classical O(N) search to O(√N). Shor’s algorithm theoretically breaks RSA, but requires fault-tolerant logical qubits [Shor, 1997].

6.3.2 Resource Estimation & Algorithm-Hardware Co-Design

Resource metrics: Qubit count, T-gate count, circuit depth, connectivity constraints.
Co-design examples: Tailoring VQE ansätze to hardware connectivity, or adapting qubit mapping to minimize long-range gates [Guerreschi & Smelyanskiy, 2017].

6.4 Variational and Hybrid Algorithms

Variational Quantum Algorithms (VQAs) and hybrid classical-quantum algorithms dominate the near-term landscape.

6.4.1 Trainability and Barren Plateaus

Barren plateaus: Exponentially vanishing gradients in parameterized circuits for random initializations, making optimization difficult [McClean et al., 2018].
Mitigation strategies: Layerwise learning, problem-inspired ansätze, local cost functions.

6.4.2 Optimizer Design

Gradient-based optimizers: Adam, L-BFGS, SPSA (Simultaneous Perturbation Stochastic Approximation).
Gradient-free optimizers: Nelder-Mead, COBYLA, suitable for noisy hardware.

6.4.3 Noise-Aware Ansätze

Designing circuits that minimize two-qubit gates or leverage hardware-native gates improves performance under NISQ noise.
Examples: Hardware-efficient ansätze for VQE, problem-specific ansätze for QAOA.

6.5 Software Stack & Compilation

Efficient compilation and software design are essential for translating high-level quantum algorithms into hardware instructions.

6.5.1 High-Level Languages

Qiskit, Cirq, PennyLane, Q#: Provide quantum programming frameworks with hybrid classical interfaces.
Features: Parameterized circuits, simulator backends, noise modeling.

6.5.2 Compilers and Transpilers

Transpilation: Maps logical circuits to physical qubits, inserting SWAPs and optimizing gate sequences.
Challenges: Connectivity constraints, noise-aware routing, and minimizing circuit depth.

6.5.3 Qubit Routing and Scheduling

Critical for architectures with limited qubit connectivity.
Techniques: Heuristic mapping, exact scheduling (SMT solvers), AI-driven optimizers [Nam et al., 2018].
Scheduling can reduce idle time, exposure to decoherence, and gate collisions.

6.5.4 Verification & Simulation Tools

ZX-calculus, symbolic simulation, assertion frameworks aid in verification of quantum circuits.
Noise-aware simulators (e.g., Qiskit Aer, PennyLane) allow benchmarking and pre-execution optimization.

6.6 Summary Table: Error and Algorithmic Challenges

Domain	Key Challenge	Current Approaches / Examples
Noise & Error Mitigation	Decoherence, gate errors, measurement noise	Zero-noise extrapolation, symmetry verification, noise-resilient circuits
Quantum Error Correction	Thresholds, high overhead	Surface codes, LDPC codes, concatenated codes, MWPM / neural decoders
Algorithms & Complexity	Quantum advantage, resource estimation	Grover, Shor, VQE, QAOA; co-design for hardware
Variational & Hybrid Algorithms	Trainability, barren plateaus, optimizer design	Layer-wise ansätze, noise-aware ansätze, SPSA, gradient-free optimizers
Software Stack & Compilation	Qubit mapping, scheduling, transpilation	Qiskit, Cirq, PennyLane; transpilers, routing, verification frameworks

References for Section 6 (examples):

Magesan, E., Gambetta, J. M., & Emerson, J. (2011). Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett., 106, 180504.
Blume-Kohout, R., Gamble, J. K., Nielsen, E., et al. (2017). Demonstration of qubit operations using gate set tomography. Nat. Commun., 8, 14485.
Temme, K., Bravyi, S., & Gambetta, J. M. (2017). Error mitigation for short-depth quantum circuits. Phys. Rev. Lett., 119, 180509.
Bonet-Monroig, X., Sagastizabal, R., Singh, R., et al. (2018). Low-cost error mitigation by symmetry verification. Phys. Rev. A, 98, 062339.
Fowler, A. G., Mariantoni, M., Martinis, J. M., et al. (2012). Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A, 86, 032324.
Cerezo, M., Arrasmith, A., Babbush, R., et al. (2021). Variational quantum algorithms. Nat. Rev. Phys., 3, 625–644.
McClean, J. R., Boixo, S., Smelyanskiy, V. N., et al. (2018). Barren plateaus in quantum neural network training landscapes. Nat. Commun., 9, 4812.
Nam, Y., Ross, N. J., Su, Y., et al. (2018). Automated optimization of large quantum circuits with continuous parameters. npj Quantum Inf., 4, 23.
Shor, P. W. (1997). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput., 26(5), 1484–1509.
Varsamopoulos, S., Criger, B., & Bertels, K. (2021). Decoding small surface codes with feedforward neural networks. Quantum Inf. Process., 20, 1–18.

7. Benchmarks, Verification & Validation

Quantum computing progress depends on measurable metrics, verification frameworks, and standardized benchmarking. Due to noise and complexity, verifying correctness and performance is critical for both NISQ and fault-tolerant systems.

7.1 Standardized Benchmarks

Gate Fidelity Benchmarks: Average single- and two-qubit gate fidelities provide baseline metrics for device performance [Kjaergaard et al., 2020].
Circuit Benchmarks: Predefined circuits (GHZ, quantum Fourier transform, QAOA instances) are used to evaluate device performance in realistic scenarios [Arute et al., 2019].
Application-Level Benchmarks: End-to-end quantum algorithms, e.g., VQE for chemistry, Grover search, provide practical metrics of quantum advantage [McArdle et al., 2020].

Table 1: Benchmark Types

Benchmark Type	Example Metrics	Target Devices	Purpose
Gate fidelity	Average gate error, process fidelity	Superconducting, ion traps	Evaluate individual gates
Circuit benchmarks	Success probability, depth-limited fidelity	All platforms	Assess realistic algorithm performance
Application benchmarks	Energy estimation accuracy, optimization score	NISQ simulators & devices	Map hardware to end-to-end tasks

7.2 Verification of Quantum Computations

Due to the exponential state space, direct verification is infeasible for large circuits. Key strategies include:

Randomized Benchmarking (RB): Measures average error rates over random Clifford sequences, providing scalable characterization [Magesan et al., 2011].
Cross-Entropy Benchmarking: Used in quantum supremacy experiments to compare experimental outputs against ideal simulations [Arute et al., 2019].
Formal Verification: Techniques like ZX-calculus and symbolic methods enable formal proof of circuit equivalence [Coecke & Duncan, 2011].

Example: Google’s Sycamore processor achieved quantum supremacy by running a random circuit benchmark in 200 seconds versus 10,000 years for a classical supercomputer [Arute et al., 2019].

8. Quantum Networks & Distributed Quantum Computing

Quantum networking allows modular quantum computers, long-distance secure communication, and distributed quantum algorithms.

8.1 Quantum Repeaters & Entanglement Distribution

Challenge: Direct fiber links lose photons over long distances.
Solution: Quantum repeaters generate and store entangled pairs to extend communication distances.
Protocols: Entanglement swapping, purification, and quantum memory integration [Wehner et al., 2018]

Table 2: Quantum Networking Techniques

Technique	Function	Example Implementation
Quantum repeater	Extend entanglement distance	NV-center, trapped-ion, cold-atom nodes
Entanglement swapping	Connect distant qubits	Modular ion traps linked via photons
Photonic interconnects	Link superconducting qubit modules	IBM, ETH Zurich experiments

8.2 Interoperability Standards

QKD standards: ETSI and ISO are defining protocols for quantum key distribution.
Modular architectures: Require consistent interfaces between nodes, including error-corrected logical qubits and synchronization protocols [Awschalom et al., 2021].

Example: China’s Micius satellite demonstrated satellite-to-ground entanglement distribution, showcasing practical long-distance quantum networking [Yin et al., 2017].

9. Applications & Domain Gaps

Quantum computing applications are emerging but constrained by hardware limitations and noise. Mapping domain problems to device capabilities is essential for practical impact.

9.1 Practical Application Domains

Quantum Chemistry & Materials: VQE, quantum phase estimation (QPE) for molecular energies [McArdle et al., 2020].
Optimization & Finance: QAOA for combinatorial optimization, portfolio optimization, risk assessment [Farhi et al., 2014].
Machine Learning & AI: Quantum kernel methods, hybrid classical-quantum models [Biamonte et al., 2017].

9.2 Mapping Problems to Hardware Limits

Domain	Algorithm	NISQ Feasible?	Hardware Constraints
Quantum Chemistry	VQE	Yes	Shallow circuits, connectivity-limited
Optimization	QAOA	Partial	Depth limited, noise affects convergence
Machine Learning	QSVM, VQC	Experimental	Requires gradient optimization, barren plateaus

9.3 End-to-End Pipelines

Problem formulation → Quantum algorithm selection → Circuit compilation → Hardware execution → Post-processing & verification.
Co-design and hybrid algorithms bridge gaps between idealized algorithms and real NISQ devices.

10. Security, Cryptography & Post-Quantum Transitions

Quantum computing poses new security challenges due to its ability to break classical public-key cryptography.

10.1 Threat Models

Shor’s algorithm can break RSA and ECC once fault-tolerant quantum computers with thousands of logical qubits exist.
Grover’s algorithm provides quadratic speedup for brute-force attacks.

10.2 Post-Quantum Cryptography (PQC) Migration

NIST PQC standards: Lattice-based (Kyber, Dilithium), code-based (McEliece), hash-based signatures.
Migration requires careful integration in enterprise and cloud infrastructure [Chen et al., 2022].

10.3 Quantum-Safe Protocols

QKD provides provable security for key distribution.
Hybrid classical-quantum protocols combine PQC with QKD for resilience.

11. Societal, Workforce & Ethical Issues

Beyond technology, societal readiness, ethical frameworks, and workforce training are essential.

11.1 Education & Workforce Development

Quantum computing requires interdisciplinary expertise: physics, computer science, engineering, and mathematics.
Universities are introducing quantum engineering courses, and industry provides training via cloud-based quantum platforms.

11.2 Standards & Policy

Standardization efforts in hardware, software, and cryptography (ETSI, ISO, NIST) are critical for interoperability and trust.
Government-funded quantum initiatives worldwide emphasize responsible innovation.

11.3 Responsible Innovation & Ethical Considerations

Privacy, security, and equitable access must guide deployment.
Consideration of environmental impact (cryogenics, fabrication energy) is increasingly relevant.
Ethics in defense applications and dual-use concerns must be proactively addressed.

Summary Table: Quantum Computing Landscape & Challenges

Domain	Key Challenges / Opportunities	Examples / References
Benchmarking & Verification	Standardized metrics, circuit verification	Randomized benchmarking, cross-entropy [Arute et al., 2019]
Quantum Networks	Repeaters, entanglement distribution, interoperability standards	Micius satellite, modular trapped-ion links
Applications & Domain Mapping	Hardware-aware problem selection, NISQ limitations	VQE, QAOA, QSVM
Security & PQC Transition	Migration to quantum-safe protocols	NIST PQC standards, hybrid classical-quantum protocols
Societal & Ethical Issues	Education, workforce, policy, responsible innovation	University programs, ETSI, ISO, NIST, ethical frameworks

References (Section 7–11)

Arute, F., Arya, K., Babbush, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574, 505–510.
McArdle, S., Endo, S., Aspuru-Guzik, A., et al. (2020). Quantum computational chemistry. Rev. Mod. Phys., 92, 015003.
Farhi, E., Goldstone, J., Gutmann, S., & Sipser, M. (2014). A quantum approximate optimization algorithm. arXiv:1411.4028.
Biamonte, J., Wittek, P., Pancotti, N., et al. (2017). Quantum machine learning. Nature, 549, 195–202.
Wehner, S., Elkouss, D., & Hanson, R. (2018). Quantum internet: A vision for the road ahead. Science, 362, eaam9288.
Awschalom, D. D., Hanson, R., Wrachtrup, J., et al. (2021). Quantum technologies for information science. Nature Photonics, 15, 345–356.
Yin, J., Cao, Y., Li, Y., et al. (2017). Satellite-based entanglement distribution over 1200 kilometers. Science, 356, 1140–1144.
Chen, L. K., Jordan, S., Liu, Y. K., et al. (2022). Report on post-quantum cryptography. NIST IR 8309.

12. Opportunities & Emerging Directions (Research & Translational)

Quantum computing research spans multiple temporal horizons, from near-term NISQ devices to fault-tolerant future systems, with opportunities in hardware, algorithms, applications, and cross-disciplinary integration. Identifying these opportunities is critical for guiding investment, research prioritization, and translational efforts.

12.1 Near-Term (NISQ) Opportunity Spaces

The Noisy Intermediate-Scale Quantum (NISQ) era (50–1,000 qubits with limited fidelity) presents opportunities despite noise constraints.

12.1.1 Quantum Chemistry and Materials Science

Applications: Variational Quantum Eigensolver (VQE) for molecular energy estimation, simulation of small molecules, and catalysts [McArdle et al., 2020].
Opportunities: Optimization of battery materials, superconductors, and photonic materials using shallow circuits tailored to NISQ devices.
Limitations: Circuit depth, qubit connectivity, and decoherence limit system size to tens of qubits.

12.1.2 Stochastic Sampling & Optimization

Applications: Quantum Approximate Optimization Algorithm (QAOA) for combinatorial optimization, portfolio optimization, traffic routing.
Example: Shallow-depth QAOA for Max-Cut problems on graphs of ~20–50 nodes demonstrates early quantum advantage in constrained settings [Farhi et al., 2014].
Opportunities: Heuristic improvement, hardware-aware ansätze, and classical-quantum hybrid solvers.

12.1.3 Machine Learning & Hybrid AI

Applications: Quantum kernel methods, hybrid classical-quantum neural networks for feature mapping [Biamonte et al., 2017].
Opportunities: Enhancing AI with quantum subroutines for feature transformation, sampling, and linear algebra in NISQ-friendly circuits.

12.2 Mid-Term Opportunities (Error-Mitigation + Early Logical Qubits)

As early logical qubits become feasible (~tens to hundreds of error-corrected qubits), research opportunities expand to error-resilient computation and scalable hybrid pipelines.

12.2.1 Error-Resilient Algorithm Design

Focus on fault-tolerant-friendly algorithmic structures such as modular VQE and QAOA with error suppression layers.
Example: Early logical qubits can perform multi-step chemistry simulations with higher accuracy, enabling realistic molecular modeling [O’Gorman et al., 2016].

12.2.2 Algorithm-Hardware Co-Design

Opportunities: Tailoring gate sequences, ansätze, and transpilation to specific logical qubit architectures to maximize computational throughput.
Example: Superconducting logical qubits with surface code layout can simulate 10–50 logical qubit circuits for chemistry or optimization applications.

12.2.3 Benchmarking and Standardization

Early logical qubits facilitate benchmarks for fault-tolerant protocols, enabling reproducibility and standardization across platforms.
Opportunity: Comparative studies between superconducting, trapped ion, and photonic logical qubits to identify optimal early architectures.

12.3 Long-Term Opportunities (Fault-Tolerant Transformative Applications)

Fault-tolerant quantum computing unlocks transformative applications previously considered intractable.

12.3.1 Cryptanalysis

Shor’s algorithm enables breaking widely deployed public-key cryptography (RSA, ECC) at scale [Shor, 1997].
Implications: Full-scale quantum computers require thousands of logical qubits and millions of T-gates to threaten real-world encryption.

12.3.2 Large-Scale Simulation

Applications: Quantum simulation of chemical reactions, complex condensed matter systems, nuclear physics, and materials.
Example: Full simulation of nitrogenase enzyme or complex transition-metal catalysts for industrial-scale chemical synthesis.

12.3.3 Optimization at Scale

Solving large combinatorial optimization problems beyond classical reach, including supply chain logistics, energy grid management, and financial risk modeling.

12.4 Cross-Cutting Opportunities

Beyond timeline-based categorization, several cross-cutting research and translational opportunities emerge:

12.4.1 AI + Quantum Computing Integration

Applications: Using AI for error correction, pulse optimization, and variational algorithm design [Cerezo et al., 2021].
Opportunity: Machine learning models can predict noise patterns, optimize qubit allocation, and accelerate compilation.

12.4.2 Quantum Sensing

Applications: High-precision sensing using NV-centers, trapped ions, or superconducting circuits for magnetic, electric, and gravitational fields.
Opportunity: Hybrid devices combining quantum computing and quantum sensing to inform feedback-based error mitigation and real-time control [Degen et al., 2017].

12.4.3 Co-Design and Hybrid Classical-Quantum Ecosystems

Co-design: Integrated hardware-software pipelines to align algorithmic structures with physical constraints.
Hybrid computation: Alternating classical and quantum processing to solve large-scale problems efficiently.
Example: Hybrid VQE-QAOA pipelines for molecular simulation or stochastic optimization.

12.5 Comparative Summary Table: Opportunities Across Time Horizons

Horizon	Key Opportunities	Representative Examples	Constraints / Research Needs
Near-Term NISQ	Quantum chemistry, VQE, QAOA, stochastic sampling	H₂O simulation, Max-Cut (20–50 qubits)	Noise, shallow circuits, connectivity limits
Mid-Term Early Logical	Error-resilient computation, co-design, benchmarking	Surface-code logical qubits (10–50 LQs)	Error correction overhead, hardware integration
Long-Term Fault-Tolerant	Cryptanalysis, large-scale simulation, combinatorial optimization	Shor’s factoring, full molecular simulations	Qubit scaling, magic state distillation, circuit depth
Cross-Cutting	AI integration, quantum sensing, hybrid ecosystems	ML-based noise mitigation, NV sensing feedback	Toolchain integration, interoperability

References (Section 12)

McArdle, S., Endo, S., Aspuru-Guzik, A., et al. (2020). Quantum computational chemistry. Rev. Mod. Phys., 92, 015003.
Farhi, E., Goldstone, J., Gutmann, S., & Sipser, M. (2014). A quantum approximate optimization algorithm. arXiv:1411.4028.
Biamonte, J., Wittek, P., Pancotti, N., et al. (2017). Quantum machine learning. Nature, 549, 195–202.
O’Gorman, J., Campbell, E., Horsman, D., et al. (2016). A blueprint for fault-tolerant quantum computation with superconducting qubits. Sci. Rep., 6, 30378.
Shor, P. W. (1997). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput., 26(5), 1484–1509.
Cerezo, M., Arrasmith, A., Babbush, R., et al. (2021). Variational quantum algorithms. Nat. Rev. Phys., 3, 625–644.
Degen, C. L., Reinhard, F., & Cappellaro, P. (2017). Quantum sensing. Rev. Mod. Phys., 89, 035002.

13. Methodologies for Research & Evaluation

Robust methodologies are essential for advancing quantum computing research. Given the experimental complexity, hardware diversity, and stochastic nature of quantum systems, researchers must follow structured experimental designs, reproducible simulation pipelines, and standardized evaluation metrics. This section outlines approaches for experimental design, simulation tools, and reproducibility resources.

13.1 Experimental Design & Reproducibility

13.1.1 Key Considerations

Designing experiments for quantum computing involves careful consideration of:

Hardware platform: Superconducting qubits, trapped ions, photonic qubits, or hybrid systems.
Noise characterization: Using randomized benchmarking (RB), gate set tomography (GST), or cross-entropy benchmarking [Magesan et al., 2011; Arute et al., 2019].
Circuit design: Choosing algorithms that are depth-limited and hardware-aware to remain feasible on NISQ devices.
Measurement protocols: Repeated sampling, error mitigation, and state tomography for accurate results.

Example: Google’s quantum supremacy experiment used cross-entropy benchmarking to evaluate a 53-qubit random circuit with ~10^6 measurements per circuit instance [Arute et al., 2019].

13.1.2 Reproducibility Best Practices

Detailed experimental logs: Record qubit calibrations, environmental conditions, and pulse sequences.
Parameter reporting: Include circuit depth, gate fidelity, connectivity, and decoherence times.
Open-source scripts: Provide code for transpilation, execution, and post-processing.
Multiple hardware verification: Replicate experiments across different devices to validate robustness.

Table 1: Experimental Design Checklist

Aspect	Best Practice	Examples / Tools
Hardware specification	Report qubit type, coherence times, gate errors	Superconducting, trapped ions, photonics
Circuit preparation	Depth-limited, connectivity-aware	QAOA, VQE, shallow chemistry circuits
Noise characterization	RB, GST, cross-entropy benchmarking	Qiskit Ignis, Cirq noise modeling
Measurement & sampling	Sufficient shots for statistical significance	≥10^3–10^6 shots per circuit
Documentation & reproducibility	Provide code, logs, calibration data	GitHub repositories, open-access pipelines

13.2 Simulation and Resource Estimation Tools

Simulation and modeling are critical for pre-hardware evaluation, resource estimation, and algorithm-hardware co-design.

13.2.1 Quantum Circuit Simulators

State-vector simulators: Exact simulation, exponential scaling; useful for <30 qubits.
- Example: Qiskit Aer, Cirq Simulator.
Density matrix simulators: Include noise models; essential for NISQ error analysis.
Tensor network simulators: Efficient for sparse entanglement; used in quantum chemistry and condensed-matter simulations.

13.2.2 Resource Estimation Tools

Qubit count estimation: Based on logical qubits, error-correcting codes, and algorithm depth.
Gate scheduling and transpilation: Simulate physical gate sequences, connectivity constraints, and error propagation.
Hybrid classical-quantum evaluation: Estimate classical computational requirements for variational optimization.

Example: Resource estimation for Shor’s algorithm factoring a 2048-bit number predicts ~20 million T-gates and ~4,000 logical qubits for full fault-tolerant implementation [Gidney & Ekerå, 2019].

13.3 Open Datasets, Benchmark Suites, and Reproducible Pipelines

13.3.1 Open Datasets

Quantum chemistry: Molecular Hamiltonians (H₂, LiH, H₂O) for benchmarking VQE and QPE.
Quantum optimization: Graph instances for Max-Cut, traveling salesman problem, QUBO datasets.
Noise and calibration: Public datasets of qubit calibrations and noise profiles (IBM Q, Rigetti, IonQ).

13.3.2 Benchmark Suites

QASMBench: Standardized benchmarks for superconducting and ion-trap devices.
SupermarQ: A suite for evaluating NISQ device performance across multiple domains (chemistry, optimization, machine learning) [Brown et al., 2022].

13.3.3 Reproducible Pipelines

Integrated software frameworks: Qiskit, PennyLane, Cirq, Q# provide consistent environments for simulation, transpilation, and execution.
Workflow automation: Continuous integration pipelines with pre-execution simulation, post-processing, and visualization for verification.
Version control & documentation: Git-based management ensures reproducibility across different research groups and hardware backends.

Table 2: Reproducibility Resources

Resource Type	Examples	Purpose
Open datasets	Qiskit chemistry datasets, QUBO graph instances	Algorithm testing, benchmarking
Benchmark suites	SupermarQ, QASMBench	Standardized cross-platform performance metrics
Simulation frameworks	Qiskit Aer, Cirq, PennyLane	Noise modeling, resource estimation
Reproducible pipelines	GitHub, automated CI/CD pipelines	End-to-end reproducibility and workflow automation

13.4 Summary

Methodologies for research and evaluation in quantum computing emphasize:

Careful experimental design to account for platform-specific noise, gate errors, and measurement limitations.
Simulation and resource estimation tools to optimize algorithms and predict feasibility prior to execution.
Open datasets and reproducible pipelines to enable cross-platform benchmarking, verification, and standardized evaluation.

Such methodological rigor ensures scientific reliability, hardware-software co-design, and community-wide reproducibility, which are essential for the advancement of quantum computing.

References (Section 13)

Arute, F., Arya, K., Babbush, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574, 505–510.
Magesan, E., Gambetta, J. M., & Emerson, J. (2011). Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett., 106, 180504.
Gidney, C., & Ekerå, M. (2019). How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum, 3, 135.
Brown, A., Murali, P., Prakash, R., et al. (2022). SupermarQ: A scalable benchmark suite for quantum computers. npj Quantum Inf., 8, 125.
McArdle, S., Endo, S., Aspuru-Guzik, A., et al. (2020). Quantum computational chemistry. Rev. Mod. Phys., 92, 015003.

14. Case Studies & Examples

Empirical demonstrations provide insight into the current capabilities and challenges of quantum computing. They also highlight translational opportunities from experimental devices to practical applications.

14.1 Quantum Advantage Experiments

Google Sycamore (2019): Demonstrated quantum supremacy by sampling the output of a 53-qubit random circuit faster than classical supercomputers. Execution time: ~200 seconds vs ~10,000 years on a classical supercomputer [Arute et al., 2019].
IBM Quantum Experiments: Demonstrated complex VQE simulations for H₂O and LiH molecules, showcasing NISQ algorithm performance on superconducting devices [Kandala et al., 2017].

Table 1: Quantum Advantage / Early Demonstration Experiments

Experiment	Platform	Qubits	Algorithm / Task	Outcome / Significance
Sycamore 2019	Superconducting	53	Random circuit sampling	First claimed quantum supremacy
IBM VQE H₂O / LiH	Superconducting	6–12	Variational Quantum Eigensolver	Early chemical simulation on NISQ hardware
IonQ Modular Network	Trapped ions	11–20	Entanglement distribution	Demonstrated deterministic long-range entanglement

14.2 Variational Quantum Eigensolver (VQE) for Small Molecules

Methodology: Parameterized ansätze are optimized with classical optimizers to minimize molecular Hamiltonians.
Examples:
- H₂ molecule (2 qubits)
- LiH molecule (4 qubits)
- BeH₂ molecule (6 qubits) [Peruzzo et al., 2014]
Significance: Demonstrates how shallow circuits and hybrid algorithms can provide practical outputs despite NISQ noise.

14.3 Error-Correction Demonstrations

Surface Code Experiments: Superconducting qubits demonstrated logical qubits with error rates lower than physical qubits [Kelly et al., 2015].
Trapped-Ion Encodings: Implementation of small repetition codes to correct bit-flip errors.
Significance: Early validation of fault-tolerant principles and threshold estimation, critical for scaling to long-term fault-tolerant devices.

15. Roadmap & Recommendations

To advance quantum computing research effectively, a structured roadmap is essential, combining hardware, algorithms, applications, workforce, and policy considerations.

15.1 Prioritized Research Directions

Priority	Focus Area	Description / Opportunities
High	Hardware Scaling & Coherence	Superconducting, trapped ions, photonics; modular architectures; cryogenics and materials optimization
High	Error Mitigation & Fault Tolerance	Development of QEC codes, noise-resilient ansätze, early logical qubits
Medium	Algorithmic Development	NISQ algorithms (VQE, QAOA), quantum machine learning, hybrid classical-quantum optimization
Medium	Benchmarking & Reproducibility	Standardized benchmarks (SupermarQ, QASMBench), simulation and verification pipelines
Low	Quantum Networking & Sensing	Quantum repeaters, entanglement distribution, precision sensing applications
Cross-Cutting	AI+QC Integration	Pulse optimization, error prediction, compilation improvements

15.2 Funding and Collaboration Suggestions

Public-Private Partnerships: Encourage collaboration between academia, national labs, and industry to share hardware, datasets, and simulators.
International Cooperation: Promote quantum networking, cryptography standardization, and multi-country benchmarking initiatives.
Targeted Funding: Prioritize NISQ-to-early logical qubit research, algorithm-hardware co-design, and fault-tolerant roadmap studies.

15.3 Policy Recommendations

Standards & Interoperability: Develop global guidelines for quantum hardware interfaces, cryptography, and cloud-based execution.
Workforce Development: Invest in interdisciplinary training programs across physics, computer science, and engineering.
Responsible Innovation: Ethical deployment, equitable access, and environmental sustainability of quantum hardware should guide public policy.

16. Conclusion

Quantum computing represents a paradigm shift in computational capability, offering transformative opportunities across chemistry, optimization, cryptography, and materials science.

Key takeaways:

Hardware Progress: Superconducting, trapped ions, photonic, and spin-based qubits each offer unique scalability and coherence trade-offs.
Algorithms & NISQ Opportunities: VQE, QAOA, quantum machine learning, and hybrid algorithms demonstrate practical potential on near-term devices.
Error Management: Noise characterization, error mitigation, and QEC are central to transitioning from NISQ to fault-tolerant systems.
Cross-Cutting Directions: AI integration, quantum networking, co-design, and reproducible methodologies accelerate translational research.
Roadmap & Policy: Coordinated investment, standardization, workforce training, and ethical frameworks are essential for sustainable growth.

Despite significant challenges, strategically guided research and collaboration can realize near-term gains while preparing for the transformative long-term impact of fully fault-tolerant quantum computers.

17. References (Full Bibliographic Entries)

Arute, F., Arya, K., Babbush, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574, 505–510.
Magesan, E., Gambetta, J. M., & Emerson, J. (2011). Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett., 106, 180504.
Peruzzo, A., McClean, J., Shadbolt, P., et al. (2014). A variational eigenvalue solver on a photonic quantum processor. Nat. Commun., 5, 4213.
Kelly, J., Barends, R., Fowler, A. G., et al. (2015). State preservation by repetitive error detection in a superconducting quantum circuit. Nature, 519, 66–69.
Kandala, A., Mezzacapo, A., Temme, K., et al. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature, 549, 242–246.
McArdle, S., Endo, S., Aspuru-Guzik, A., et al. (2020). Quantum computational chemistry. Rev. Mod. Phys., 92, 015003.
Farhi, E., Goldstone, J., Gutmann, S., & Sipser, M. (2014). A quantum approximate optimization algorithm. arXiv:1411.4028.
Biamonte, J., Wittek, P., Pancotti, N., et al. (2017). Quantum machine learning. Nature, 549, 195–202.
O’Gorman, J., Campbell, E., Horsman, D., et al. (2016). A blueprint for fault-tolerant quantum computation with superconducting qubits. Sci. Rep., 6, 30378.
Gidney, C., & Ekerå, M. (2019). How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum, 3, 135.
Brown, A., Murali, P., Prakash, R., et al. (2022). SupermarQ: A scalable benchmark suite for quantum computers. npj Quantum Inf., 8, 125.
Degen, C. L., Reinhard, F., & Cappellaro, P. (2017). Quantum sensing. Rev. Mod. Phys., 89, 035002.
Chen, L. K., Jordan, S., Liu, Y. K., et al. (2022). Report on post-quantum cryptography. NIST IR 8309.
Wehner, S., Elkouss, D., & Hanson, R. (2018). Quantum internet: A vision for the road ahead. Science, 362, eaam9288.

References

Preskill, J. (2018). Quantum computing in the NISQ era and beyond. Quantum. — Defines the NISQ era and its implications. arXiv
Arute, F. et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature — Google’s Sycamore experiment (quantum supremacy claim). Nature
Zhong, H.-S., Wang, H., Deng, Y.-H., et al. (2020). Quantum computational advantage using photons. Science — Photonic demonstration of quantum advantage (Jiuzhang). Wikipedia+1
Linke, N. M., et al. (2017). Experimental comparison of two quantum computing architectures. PNAS — comparative hardware insights (ion traps vs superconducting). PNAS
Variational quantum algorithms: reviews and surveys (2024). Example: Variational quantum algorithms: fundamental concepts, analyses and applications (2024 review). — Good survey of VQAs, their challenges (trainability, noise). SpringerLink
Quantum error correction — Recent progress: Quantum error correction below the surface code threshold (Nature, 2024) — shows experimental advances and thresholds. Nature
Quantum machine learning reviews (2018–2024). Example: Zeguendry et al. (2023). Quantum Machine Learning: A Review and Case Studies. — Surveys QML state and challenges. PMC
Systematic reviews & surveys on QC capabilities and hardware (2017–2025). Example: comparative qubit technology reviews (2024–2025). Preprints+1
Recent literature reviews on QML and VQA systematic analyses (2024, 2025) — useful for “opportunities” and algorithmic limits. ScienceDirect+1
Industry roadmaps and milestone reports (IBM roadmap 2020; various company updates) — context on scaling & industry targets. Axios