1. Classical vs Quantum Representation
Classical 2-Bit Example
In classical computing, information is represented using bits, where each bit can exist in one of two possible states — 0 or 1.
A system with two bits can represent four distinct states:
| Bit Combination | Binary | Decimal Equivalent |
|---|---|---|
| 00 | 0 | 0 |
| 01 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
Each bit combination corresponds to a unique decimal value between 0 and 3. Importantly, a classical system can exist in only one of these states at any given time.
For example:
If we have two classical bits, and their values are 0 and 1, the system is in state 01.
It cannot simultaneously represent 10 or 11. This deterministic nature limits classical computing to sequential state exploration.
Quantum 2-Qubit System
Quantum computing introduces a new paradigm based on the principles of superposition and quantum parallelism. A qubit (quantum bit) is the fundamental unit of quantum information. Unlike a classical bit that can be either 0 or 1, a qubit can exist in a superposition of both 0 and 1 simultaneously. For a two-qubit system, the possible basis states are the same as the classical combinations:
∣00⟩,∣01⟩,∣10⟩,∣11⟩
However, in quantum computing, the state of the system can be a linear combination of all these basis states:
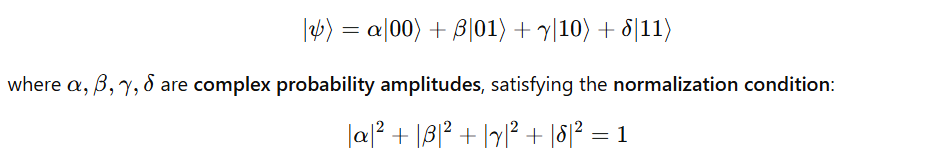
This means that a two-qubit system can represent all four states simultaneously, until measured.
Upon measurement, the system collapses to one of these states, with probabilities given by the squares of their respective amplitudes.
2. Representation of Qubits
To mathematically describe qubits, we use state vectors in a complex Hilbert space.
State Vector Representation
A state vector represents the quantum state of a system and contains the probability amplitudes of each possible outcome.
Example: A Quantum Coin
Consider a quantum coin that can exist in a superposition of Head (H) and Tail (T).
If the coin is in the Head state, we can write:

If the coin is in the Tail state, we represent it as:

Thus, the general state of the coin can be expressed as a superposition:
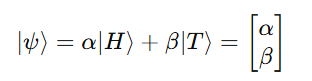
where α and β are complex numbers that satisfy:
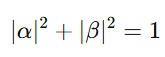
This state vector expresses the probability of being in Head or Tail state — analogous to being in 0 or 1 state in a qubit.
3 Dirac Notation (Bra-Ket Notation)
Dirac notation, introduced by Paul Dirac, provides a convenient and elegant way to represent quantum states and their operations.
It simplifies matrix and vector operations used in quantum mechanics.
Basic Components
- Ket (|ψ⟩) : Represents a column vector — the quantum state itself.
Example:
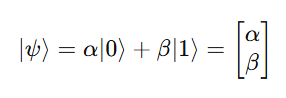


4. Common Qubit States
Here are the most frequently used qubit states in quantum computing:

5. Measurement in Qubit Notation
When a qubit is measured, it collapses from its superposition into one of the basis states.
If a qubit is in state:
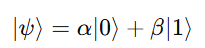
then upon measurement:

The measurement process destroys the superposition and leaves the qubit in the observed state
Example
Suppose
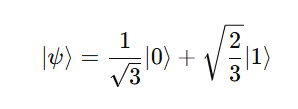
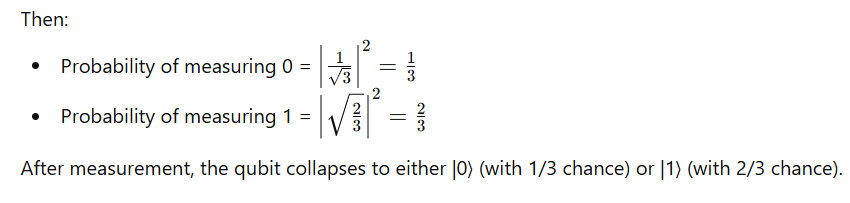
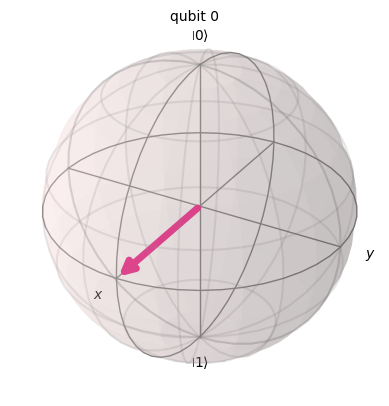
6. Visualization on the Bloch Sphere
Every single qubit state can be visualized on a Bloch Sphere, a 3D representation of the state space.
The general qubit state:
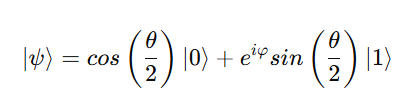
corresponds to a point on the sphere defined by:
- θ (theta): polar angle
- φ (phi): azimuthal angle
This representation is powerful for visualizing quantum gates, rotations, and state transformations.
7. Summary
- Classical bits can exist in one state at a time, while qubits can exist in superposition.
- Dirac notation provides a compact mathematical way to describe quantum states.
- State vectors and amplitudes define probabilities of measurement outcomes.
- Measurement collapses the qubit to one basis state.
- The Bloch sphere helps visualize any single-qubit state geometrically.
8. Qiskit Example
from qiskit import QuantumCircuit
from qiskit.visualization import plot_bloch_multivector
from qiskit.quantum_info import Statevector
# Create a single qubit quantum circuit
qc = QuantumCircuit(1)
# Apply Hadamard gate to create superposition
qc.h(0)
qc.draw('mpl')
# Get the statevector
state = Statevector.from_instruction(qc)
plot_bloch_multivector(state)