The Quantum Circuit Model is the standard mathematical and conceptual framework used to describe how quantum computers perform computations.
It is the quantum analog of the classical logic circuit model — but instead of using bits and irreversible logic gates, it uses qubits and reversible unitary gates that follow the principles of quantum mechanics.
In this model, a computation is represented as a sequence of quantum gates acting on a quantum register (a collection of qubits), followed by a measurement step that converts quantum information into classical results.
1. Overview of the Quantum Circuit Model
Core Idea
A quantum computation is expressed as:

2. Key Components of the Quantum Circuit Model
1. Quantum Register
A quantum register is a collection of n qubits, each capable of existing in a superposition of |0⟩ and |1⟩.
The total state of the register is a 2ⁿ-dimensional complex vector in a Hilbert space:
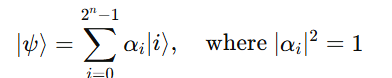
2. Quantum Gates
Quantum gates are unitary matrices that manipulate the quantum state.
They act on one or more qubits, changing their amplitudes and phases.
Examples:
- Single-qubit gates: Hadamard (H), Pauli-X, Z, S, T
- Multi-qubit gates: CNOT, CZ, Toffoli, SWAP
Each gate corresponds to a rotation or transformation in the system’s Hilbert space.
3. Measurement
At the end of computation, qubits are measured in the computational basis.
The quantum state collapses probabilistically into a classical bitstring.
Repeated runs of the same circuit give statistical distributions of outcomes.
3. Mathematical Representation
State Evolution
The evolution of a quantum register under a quantum circuit is given by:

This output represents a superposition — the qubit is equally likely to be 0 or 1 upon measurement.
4. Circuit Diagram Representation
Quantum circuits are represented visually using circuit diagrams, where:
- Horizontal lines → qubits
- Boxes or symbols → quantum gates
- Time flows left → right
- Vertical connections → multi-qubit operations (entanglement)
Example: Bell State Circuit
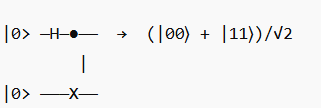
- Apply Hadamard (H) on qubit 1 → creates superposition
- Apply CNOT → entangles qubit 1 and 2
- Resulting state → Bell state, maximally entangled
This is a fundamental example of the quantum circuit model in action.
5. Features and Principles of the Quantum Circuit Model
(a) Superposition
A quantum circuit can represent and process all possible inputs simultaneously, since a register of n qubits encodes 2ⁿ states in superposition.
(b) Entanglement
Quantum gates can create non-classical correlations between qubits, where measurement outcomes are dependent — enabling quantum teleportation, quantum cryptography, and speedups in algorithms.
(c) Interference
Quantum circuits exploit constructive and destructive interference of probability amplitudes to amplify correct solutions and suppress incorrect ones — as in Grover’s algorithm.
(d) Reversibility
All gates in the model are unitary, meaning no information is destroyed.
This is in contrast to classical circuits, where AND/OR gates are irreversible.
6. Universal Quantum Computation
The Quantum Circuit Model provides a foundation for universal computation — any unitary operation on n qubits can be approximated using a finite set of basic gates.
Universal Gate Set Examples
- {Hadamard (H), Phase (S), π/8 (T), CNOT}
- {H, Rz(θ), CNOT}
This property makes the model both theoretically complete and practically implementable across different quantum hardware platforms.
7. Example: Quantum Circuit Model for Grover’s Algorithm
Grover’s algorithm (for searching unsorted databases) can be expressed as a quantum circuit:
- Initialize all qubits to |0⟩.
- Apply Hadamard gates → create uniform superposition.
- Apply Oracle Circuit → inverts the phase of the target state.
- Apply Diffusion Operator → amplifies probability of the correct state.
- Measure → observe the target with high probability.
This entire process can be written as:
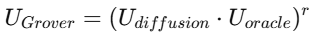
where r is the number of iterations.
Each U corresponds to a specific quantum sub-circuit, forming the overall quantum computation.
Comparison: Circuit Model vs Other Quantum Models
| Feature | Quantum Circuit Model | Adiabatic / Annealing Model | Measurement-Based (Cluster-State) |
|---|---|---|---|
| Computation Type | Discrete sequence of gates | Continuous evolution | Series of adaptive measurements |
| Representation | Quantum gates + circuits | Hamiltonian evolution | Entangled cluster state |
| Example Systems | IBM, Google QCs | D-Wave (Quantum Annealer) | Photonic and optical systems |
| Universality | Fully universal | Equivalent with mapping | Fully universal |
| Ease of Programming | High (circuit-based SDKs) | Moderate | Complex |
Most modern quantum computers — including those by IBM, Google, and Rigetti — use the Quantum Circuit Model as their operational foundation.
9. Circuit Depth and Complexity
Two key parameters define circuit performance:
- Circuit Width (n): number of qubits used.
- Circuit Depth (d): number of sequential gate layers.
Quantum algorithms aim to minimize depth (for faster, lower-error computation) while maximizing the computational space (2ⁿ possible states).
Circuit optimization involves reducing redundant gates, parallelizing operations, and mapping logical qubits efficiently onto hardware qubits.
10. Advantages of the Quantum Circuit Model
✅ Universality — Can represent any quantum algorithm.
✅ Hardware Compatibility — Aligns with gate-based quantum computers (IBM, Google, etc.).
✅ Flexibility — Can simulate any unitary process.
✅ Programmability — Easily implemented in quantum programming languages (Qiskit, Cirq).
✅ Visual Clarity — Circuit diagrams offer intuitive understanding of operations.
11. Challenges and Limitations
⚠️ Noise and Decoherence: Real gates are imperfect and introduce errors.
⚠️ Scalability: Current hardware supports limited circuit depth and qubit count.
⚠️ Error Correction Overhead: Requires many physical qubits per logical qubit.
⚠️ Compilation Complexity: Translating high-level algorithms into hardware-compatible circuits is nontrivial.
Despite these challenges, the quantum circuit model remains the dominant paradigm for quantum algorithm design and execution.
Summary
| Aspect | Quantum Circuit Model |
|---|---|
| Definition | Framework describing quantum computation as sequences of unitary gates and measurements |
| State Representation | Vector in 2ⁿ-dimensional Hilbert space |
| Computation | Sequential application of gates (U₁, U₂, …, Uₖ) |
| Measurement | Converts quantum states into classical outputs |
| Core Features | Superposition, entanglement, interference, reversibility |
| Universality | Any quantum algorithm can be represented as a circuit |
| Example Implementations | IBM Quantum, Google Sycamore, Rigetti Aspen |
| Applications | Shor’s Algorithm, Grover’s Search, Quantum Fourier Transform |
13. Conclusion
The Quantum Circuit Model is the foundation of modern quantum computing.
It provides a precise and versatile way to represent quantum computations through sequences of reversible transformations applied to qubits.
By combining superposition, entanglement, and interference, the model captures the unique advantages of quantum information processing — enabling algorithms that outperform classical systems in specific domains.


