1. Introduction
In classical computing, information is represented using bits, which can exist in one of two definite states: 0 or 1. Every computational process in a classical system is built on these binary digits. However, in quantum computing, information is stored in quantum bits, or qubits, which leverage the fundamental principles of quantum mechanics — such as superposition and entanglement. This enables quantum computers to perform certain computations much more efficiently than classical systems.
This chapter explores how qubit states differ from classical bit states, examines their mathematical representation, and discusses how increasing the number of qubits exponentially expands the computational possibilities of a quantum computer.
2. Classical Bits and Their States
In a classical computing system, each bit can have a definite value of either 0 or 1.
When multiple bits are used, they can represent a combination of these values.
Example: Two Classical Bits
- With two bits, there are four possible states:
00, 01, 10, and 11, which correspond to decimal values 0, 1, 2, and 3, respectively. - Each bit is always in a definite state—either 0 or 1.
- The system can exist in only one of these states at a time.
Hence, a classical 2-bit system at any given moment may represent only one value from {00, 01, 10, 11}. To explore all possible combinations, it must process each state sequentially.
3. Quantum Bits (Qubits)
A qubit is the quantum analog of a classical bit, but with a fundamental difference: it can exist in a superposition of both |0⟩ and |1⟩ states simultaneously.
Mathematical Representation of a Single Qubit
A qubit’s state can be written as: ∣ψ⟩=α∣0⟩+β∣1⟩
where:
- α and β are complex probability amplitudes,
- and satisfy the normalization condition: ∣α∣^2 + ∣β∣^2 = 1
Here, ∣α∣^2 represents the probability of measuring the qubit in state |0⟩, and ∣β∣^2 represents the probability of measuring it in state |1⟩.
Before measurement, however, the qubit exists in a superposition of both |0⟩ and |1⟩, embodying both possibilities at once.
4. Multi-Qubit Systems and Exponential Growth of States
When multiple qubits are combined, the number of possible quantum states grows exponentially with the number of qubits.
| N-Qubits | Number of States | Examples of States | Applications |
|---|---|---|---|
| 1 | (2^1 = 2) | |0⟩ and |1⟩ | A single qubit can be used as a highly sensitive quantum sensor to measure magnetic fields, electric fields, temperature, pressure and other quantities with extremely high precision |
| 2 | (2^2 = 4) | |00⟩, |01⟩, |10⟩, and |11⟩ | Used to create entangled states, such as the Bell state 1/sqrt(2)*(∣00⟩+∣11⟩). |
| 3 | (2^3 = 8) | |000⟩, |001⟩, |010⟩, |011⟩, |100⟩, |101⟩, |110⟩, and |111⟩ | A 3-qubit quantum computer can be used to simulate the behavior of a simple molecule like hydrogen (H2) |
| 4 | (2^4 = 16) | |0000⟩, |0001⟩, |0010⟩, |0011⟩, |0100⟩, |0101⟩, |0110⟩, |0111⟩, |1000⟩, |1001⟩, |1010⟩, |1011⟩, |1100⟩, |1101⟩, |1110⟩, and |1111⟩. | A 4-qubit computer can be used to implement Grover’s algorithm, which searches an unsorted database |
| 8 | (2^8 = 256) | All 256 Combinations | An 8-qubit quantum computer can be used to factor large numbers using Shor’s algorithm, |
| 30 | (2^{30} ≈ 1 billion | All 1billion combinations | Could be used to simulate the behavior of complex molecules and materials, which is crucial for developing new drugs, batteries, and other technologies |
As the table shows, each additional qubit doubles the number of possible states, leading to an exponential scaling of the system’s representational capacity.
5. Example: The Two-Qubit System
In a quantum 2-qubit system, both qubits can exist in a superposition of their individual states.
Thus, the entire system can represent a superposition of all four classical states simultaneously:
∣00⟩, ∣01⟩, ∣10⟩, and ∣11⟩
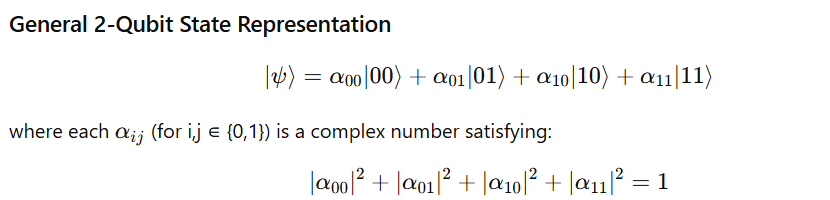
This means the two qubits collectively exist in a superposition of all four states, and measurement collapses this superposition to one definite outcome, with probabilities determined by the amplitudes.
6. Entanglement and Correlated States
When two or more qubits interact, they can become entangled, forming a composite state that cannot be described by the individual qubits alone.
An example of an entangled state is the Bell state:
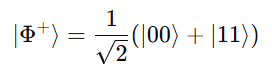
In this state, measuring the first qubit instantly determines the outcome of the second, no matter the distance between them — a phenomenon known as quantum entanglement. This property underpins the power of quantum algorithms and secure quantum communication.
7. Practical Significance of Qubit States
Quantum computers exploit the superposition and entanglement of qubit states to perform parallel computations.
For example:
- 1 qubit → high-precision quantum sensors.
- 2 qubits → creation of entangled pairs (Bell states).
- 3–4 qubits → quantum algorithms like Grover’s for database searching.
- 8 qubits → factoring numbers using Shor’s algorithm.
- 30 qubits and beyond → simulation of complex molecules and materials, aiding the design of new drugs, advanced batteries, and quantum materials.
8. Conclusion
Qubits represent the fundamental unit of quantum information, offering a revolutionary way of encoding and processing data. Unlike classical bits, which are strictly binary, qubits exploit the principles of quantum superposition and entanglement, enabling massive parallelism and powerful computational capabilities.
As quantum technologies continue to evolve, understanding qubit states and their properties will remain central to advancing quantum computing, communication, and sensing applications.


