1. Introduction
At the core of quantum mechanics lies the Schrödinger Equation, a mathematical framework describing how the quantum state of a physical system evolves over time. Proposed by Erwin Schrödinger in 1926, it provides the foundation for understanding the behavior of atoms, molecules, and subatomic particles — and, by extension, the principles that govern quantum computation.
In quantum computing, information is encoded in quantum states (|ψ⟩) represented by qubits, which evolve through controlled transformations known as unitary operations. The time evolution of these states is precisely governed by the time-dependent Schrödinger equation, making it a cornerstone for quantum circuit design, quantum simulation, and quantum algorithm development.
2. Theoretical Background
2.1 Classical vs. Quantum Dynamics
In classical mechanics, a system’s state is defined by deterministic parameters — position and momentum — evolving according to Newton’s laws of motion.
In contrast, quantum systems are described probabilistically by a wave function, denoted as ψ(r, t), representing the amplitude of finding a particle at position r and time t.
Where classical physics uses the equation
F=ma,
quantum physics uses the Schrödinger equation to describe the evolution of ψ over time.
3. The Schrödinger Equation: Mathematical Formulation
The general time-dependent Schrödinger equation (TDSE) is written as:
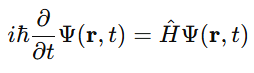
where:

Here, ∇^2 is the Laplacian operator representing kinetic energy, and V(r) represents potential energy.
4. The Time-Independent Schrödinger Equation
For stationary systems (where potential does not depend on time), we can separate variables as:
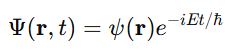
Substituting this into the TDSE gives the time-independent Schrödinger equation (TISE):
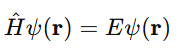
Here, E represents energy eigenvalues, and ψ(r) are eigenfunctions. This equation forms the basis for calculating the energy levels of atoms and molecules — essential in quantum simulation and quantum chemistry applications.
5. Quantum States and Qubits
In quantum computing, a qubit is analogous to a two-level quantum system, such as the spin of an electron or the polarization of a photon.

6. Role of the Schrödinger Equation in Quantum Computing
6.1 State Evolution in Quantum Circuits
Every quantum computation can be viewed as a controlled evolution of the quantum state under specific Hamiltonians. For example:

The Schrödinger equation thus provides the theoretical underpinning of quantum gate operations.
6.2 Quantum Simulation
One of the most powerful applications of quantum computers is quantum simulation — simulating the Schrödinger equation of complex systems that classical computers cannot handle.
For instance, simulating molecular energies using:
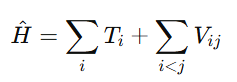
becomes exponentially hard for classical systems but polynomial on a quantum computer.
Algorithms such as Trotter-Suzuki decomposition and Variational Quantum Eigensolver (VQE) use approximations of e^{-iHt} to evolve quantum states and estimate ground state energies efficiently.
6.3 Quantum Algorithms
The Schrödinger equation’s linear and unitary nature forms the basis of quantum algorithms, such as:
- Quantum Phase Estimation (QPE) — determines eigenvalues EEE of a Hamiltonian (used in chemistry and physics simulations).
- Adiabatic Quantum Computing (AQC) — slowly evolves a Hamiltonian from H0 to H1 such that:
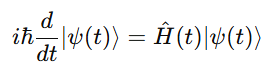
ensuring the system remains in its ground state throughout the evolution.
- Quantum Annealing — a practical form of adiabatic computing used by D-Wave systems to solve optimization problems.
7. Numerical Solutions and Simulation Approaches
Solving the Schrödinger equation analytically is possible only for simple systems (e.g., hydrogen atom, harmonic oscillator). For complex systems, numerical techniques and quantum algorithms are employed:
| Method | Approach | Quantum Application |
|---|---|---|
| Finite Difference Method (FDM) | Discretizes space and time | Quantum chemistry simulations |
| Matrix Diagonalization | Finds eigenvalues of Hamiltonian matrices | Energy-level computation |
| Quantum Variational Algorithms (VQE, QAOA) | Hybrid methods optimizing quantum circuits | Ground-state energy estimation |
| Trotterization / Lie Product Formula | Approximates ( e^{-iHt} ) | Quantum time evolution |
Quantum computers naturally perform these operations since the unitary evolution operator is inherently quantum mechanical.
8. Visualization: The Bloch Sphere and Schrödinger Evolution
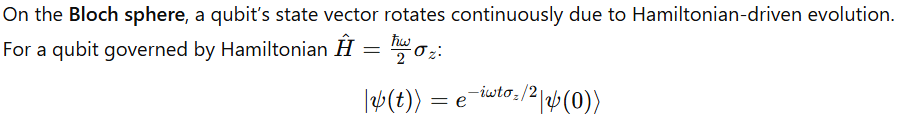
This corresponds to a rotation about the z-axis with angular frequency ω.
Hence, visualizing Schrödinger evolution on the Bloch sphere helps interpret gate actions, superpositions, and interference effects in quantum algorithms.
9. Real-World Applications
The Schrödinger equation forms the theoretical backbone of several quantum technologies:
| Domain | Application | Role of Schrödinger Equation |
|---|---|---|
| Quantum Chemistry | Energy spectra, reaction dynamics | Describes molecular wavefunctions |
| Quantum Simulation | Modeling quantum materials | Evolves multi-particle wavefunctions |
| Quantum Hardware | Superconducting qubits, trapped ions | Models system Hamiltonians |
| Quantum Algorithms | Adiabatic, phase estimation | Time-dependent evolution modeling |
| Quantum AI | Quantum neural networks | Continuous evolution of quantum states |
10. Challenges and Outlook
Despite its elegance, applying the Schrödinger equation to large-scale quantum systems poses significant challenges:
- Exponential Complexity: Classical computation of Ψ\PsiΨ scales exponentially with the number of particles.
- Decoherence: Real quantum systems deviate from ideal Schrödinger evolution due to environmental noise.
- Approximation Errors: Discretization and Trotterization can introduce computational errors.
Nevertheless, quantum hardware and hybrid algorithms are rapidly evolving to make real-time Schrödinger simulations feasible. The equation remains not only a theoretical foundation but also a computational blueprint for future quantum technologies.
Analogy to Newton’s Laws:

11. Conclusion
The Schrödinger equation serves as the mathematical soul of quantum computing, linking the physics of wave mechanics with the logic of computation. Every qubit operation, gate transformation, and quantum algorithm is, at its core, an engineered solution to this equation.
As quantum processors grow in scale and stability, solving complex time-dependent Schrödinger equations will unlock new frontiers in chemistry, materials science, optimization, and artificial intelligence — realizing the original vision of Schrödinger’s wave mechanics as a living, computational reality.



