A Quantum Algorithm is a set of instructions or procedures that a quantum computer follows to solve a problem by exploiting the principles of superposition, entanglement, and quantum interference.
In essence, a quantum algorithm is the quantum counterpart of a classical algorithm, but it operates on qubits instead of bits and performs computation using quantum gates arranged in a quantum circuit.
Quantum algorithms allow quantum computers to perform certain tasks exponentially or quadratically faster than classical computers.
1.Classical vs Quantum Algorithms
| Feature | Classical Algorithm | Quantum Algorithm |
|---|---|---|
| Data Type | Bits (0 or 1) | Qubits ( |
| Computation Type | Deterministic or probabilistic | Reversible and unitary (interference-based) |
| Parallelism | Sequential processing | Quantum parallelism (many states at once) |
| Key Resource | Time and memory | Coherence and entanglement |
| Output | Single deterministic result | Probabilistic outcomes (statistical interpretation) |
While classical algorithms process one possible input at a time, quantum algorithms process all possible inputs simultaneously through superposition, then use interference to amplify the correct results.
2. Fundamental Principles Behind Quantum Algorithms
Quantum algorithms derive their power from three key phenomena:
(a) Superposition
A register of n qubits can represent 2ⁿ possible states simultaneously. This enables quantum parallelism — evaluating many inputs at once.
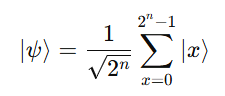
(b) Entanglement
Entanglement links qubits so that their states become correlated.
Changes to one qubit affect others instantaneously within the same quantum system — crucial for multi-qubit operations and speedups.
(c) Quantum Interference
Quantum amplitudes can interfere constructively or destructively.
Algorithms are designed so that incorrect paths cancel out and correct answers amplify, making them more likely upon measurement.
3. Structure of a Quantum Algorithm
3. Structure of a Quantum Algorithm
Most quantum algorithms follow a common logical structure:
- Initialization
Prepare all qubits in a known initial state (usually |0⟩⊗ⁿ). - Superposition Creation
Apply Hadamard gates (H) or similar to put the qubits into a superposition of all possible inputs. - Unitary Transformation (Oracle / Operator)
Apply problem-specific quantum gates that encode the problem into phase or amplitude changes (the oracle or unitary operator). - Interference / Amplification
Use interference to amplify correct results and suppress incorrect ones (e.g., Grover diffusion operator). - Measurement
Measure the quantum register to extract classical outcomes, which reveal the solution with high probability.
4. Classification of Quantum Algorithms
Quantum algorithms can be grouped into four main categories based on their computational goals:
1. Search and Optimization Algorithms
Designed to find specific items or optimal solutions faster than classical methods.
Examples:
- Grover’s Algorithm — searches an unsorted database in √N time.
- Quantum Approximate Optimization Algorithm (QAOA) — hybrid quantum-classical optimization.
- Quantum Annealing (D-Wave) — finds minima of energy landscapes.
2. Algebraic and Number-Theoretic Algorithms
These algorithms exploit quantum Fourier transforms to solve mathematical problems efficiently.
Examples:
- Shor’s Algorithm — factors large integers in polynomial time.
- Quantum Phase Estimation (QPE) — estimates eigenvalues of unitary operators.
- Discrete Logarithm Algorithm — breaks classical cryptography schemes.
3. Simulation and Modeling Algorithms
Quantum systems can simulate other quantum systems exponentially faster than classical ones.
Examples:
- Quantum Simulation of Molecules and Materials (used in chemistry, physics).
- Variational Quantum Eigensolver (VQE) — finds ground-state energies.
- Quantum Monte Carlo Simulation — stochastic quantum system modeling.
4. Machine Learning and AI-Oriented Algorithms
Quantum algorithms that enhance classical machine learning.
Examples:
- Quantum Support Vector Machine (QSVM)
- Quantum Principal Component Analysis (qPCA)
- Quantum Neural Networks (QNN)
- Amplitude Estimation Algorithms (speed up statistical sampling).
5. Important Quantum Algorithms Explained
Let’s briefly look at the three most influential quantum algorithms in history.
5.1. Shor’s Algorithm (1994)
Purpose:
Efficiently factor large integers — a task considered computationally hard for classical computers.
Why It Matters:
It can break RSA encryption, the foundation of modern internet security.
Steps:
- Prepare qubits in superposition.
- Apply a modular exponentiation operation as a quantum circuit.
- Perform Quantum Fourier Transform (QFT) to find the period of a function.
- Use that period to compute factors of the integer.
Complexity:
- Classical: exponential time.
- Quantum: Polynomial time (≈ O((log N)³)).
Impact:
Shor’s Algorithm is the primary reason for developing post-quantum cryptography.
5.2. Grover’s Algorithm (1996)
Purpose:
Search an unsorted database or solve unstructured search problems.
Why It Matters:
It provides a quadratic speedup — finding the correct item in √N steps rather than N.
Steps:
- Create superposition over all possible inputs.
- Apply oracle that marks the desired state by inverting its phase.
- Apply diffusion operator to amplify the correct state.
- Measure to retrieve the correct item with high probability.
Complexity:
- Classical: O(N)
- Quantum: O(√N)
Applications:
Database search, optimization, cryptography (key search).
5.3. Quantum Fourier Transform (QFT)
Purpose:
Transforms quantum states between time and frequency domains — key to algorithms like Shor’s and Phase Estimation.
Operation: For n qubits:
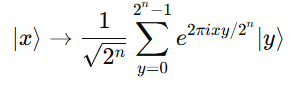
Why It Matters:
It’s the quantum analog of the classical discrete Fourier transform but can be performed exponentially faster.
Applications:
- Shor’s Algorithm
- Quantum Phase Estimation
- Signal analysis and pattern recognition.
6. Hybrid Quantum-Classical Algorithms
Due to hardware limitations (noisy, small qubit counts), hybrid algorithms combine quantum and classical computation.
Examples:
- VQE (Variational Quantum Eigensolver):
Quantum circuit prepares a parameterized state → classical optimizer adjusts parameters to minimize energy. - QAOA (Quantum Approximate Optimization Algorithm):
Alternates between quantum evolution and classical optimization to solve combinatorial problems.
These algorithms are practical today on NISQ (Noisy Intermediate-Scale Quantum) devices.
7. Quantum Speedup and Complexity
Quantum algorithms achieve speedups because they operate in Hilbert space (exponentially large state space).
| Algorithm | Problem | Classical Complexity | Quantum Complexity | Speedup |
|---|---|---|---|---|
| Shor’s | Integer factorization | Exponential | Polynomial | Exponential |
| Grover’s | Unstructured search | N | √N | Quadratic |
| QFT | Fourier transform | O(N log N) | O((log N)²) | Exponential |
| QPE | Phase estimation | Exponential | Polynomial | Exponential |
| VQE / QAOA | Optimization | Heuristic | Heuristic | Hardware-efficient |
8. Visualization of a Generic Quantum Algorithm
Circuit Flow:
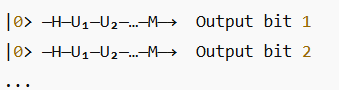
Where:
- H: Hadamard gates (create superposition)
- U₁, U₂,…: Problem-specific unitary operations (oracles)
- M: Measurement yielding classical output
This structure is the essence of the quantum circuit model of computation.
9. Challenges in Designing Quantum Algorithms
Even though quantum algorithms offer theoretical speedups, designing them remains difficult due to:
- Limited qubit count in current hardware.
- Noisy gates and decoherence reducing reliability.
- Complexity of mapping classical problems into quantum form.
- Need for reversible, unitary formulations (unlike classical logic).
Thus, most research focuses on hybrid, variational, and domain-specific algorithms until fault-tolerant quantum hardware becomes available.
10. Summary
| Aspect | Quantum Algorithms |
|---|---|
| Definition | Step-by-step procedures using qubits and quantum gates to solve problems |
| Core Principles | Superposition, entanglement, interference |
| Computation Model | Quantum circuit model (unitary transformations + measurement) |
| Categories | Search, algebraic, simulation, machine learning |
| Key Algorithms | Shor’s, Grover’s, QFT, VQE, QAOA |
| Speedup | Exponential or quadratic over classical algorithms |
| Current Stage | Early NISQ-era implementations, hybrid designs |
| Applications | Cryptography, chemistry, optimization, AI |
11. Conclusion
Quantum algorithms are the software heart of quantum computing.
They translate the strange laws of quantum mechanics into computational power — turning superposition into parallelism and interference into problem-solving.
Algorithms such as Shor’s and Grover’s have already proven that quantum computation can surpass classical limits in principle.
Newer hybrid approaches like VQE and QAOA are paving the way for near-term quantum advantage on real hardware.
As quantum computers scale up, quantum algorithm design will define the next era of technological progress — driving breakthroughs in cryptography, materials science, optimization, and artificial intelligence.


