A Quantum Gate is the basic building block of quantum computation, analogous to a logic gate in classical computers.
However, while classical gates operate on bits that can be 0 or 1, quantum gates operate on qubits, which can exist in a superposition of both states.
Quantum gates is a mathematical operation that acts on the state of one or more qubits, and it can be represented by a matrix.
Quantum gates perform unitary transformations on qubit states, meaning they are reversible and preserve total probability.
These transformations manipulate the amplitude and phase of quantum states on the Bloch sphere, allowing computation through controlled quantum interference.
1. Classical vs Quantum Gates
| Feature | Classical Logic Gate | Quantum Gate |
|---|---|---|
| Input | Bits (0 or 1) | Qubits ( |
| Output | Deterministic (one value) | Probabilistic (superposed state) |
| Operation Type | Irreversible (e.g., AND, OR) | Reversible (unitary transformation) |
| Mathematical Representation | Boolean function | Unitary matrix (U) |
| Example | AND, OR, NOT | Hadamard, Pauli-X, CNOT |
Unlike classical gates, quantum gates must always be reversible, because quantum mechanics forbids destroying information. Therefore, gates like AND or OR (which lose input information) have no direct quantum equivalent.
2. Mathematical Foundation
A quantum gate acting on a single qubit can be represented as a 2×2 unitary matrix UUU satisfying:

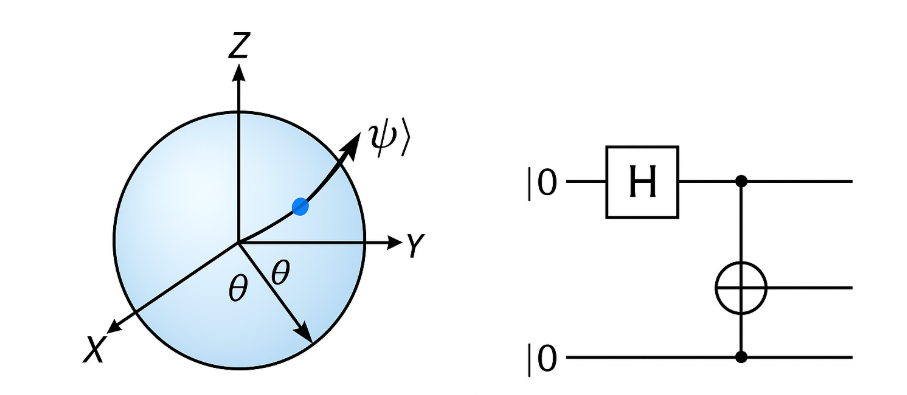
3. Visualization – The Bloch Sphere
For a single qubit, quantum gates correspond to rotations on the Bloch sphere — a 3D geometric representation of qubit states.
- The north pole represents |0⟩,
- The south pole represents |1⟩,
- Any point on the sphere represents a superposition α∣0⟩+β∣1⟩\alpha|0⟩ + \beta|1⟩α∣0⟩+β∣1⟩.
Quantum gates can rotate the qubit state vector around any axis (X, Y, Z), or apply phase shifts and reflections.
4. Types of Quantum Gates
Quantum gates are categorized based on how many qubits they act on:
4.1. Single-Qubit Gates
These gates act on a single qubit and perform rotations or phase changes on its state.
(a) Pauli Gates
The Pauli matrices represent fundamental quantum operations.

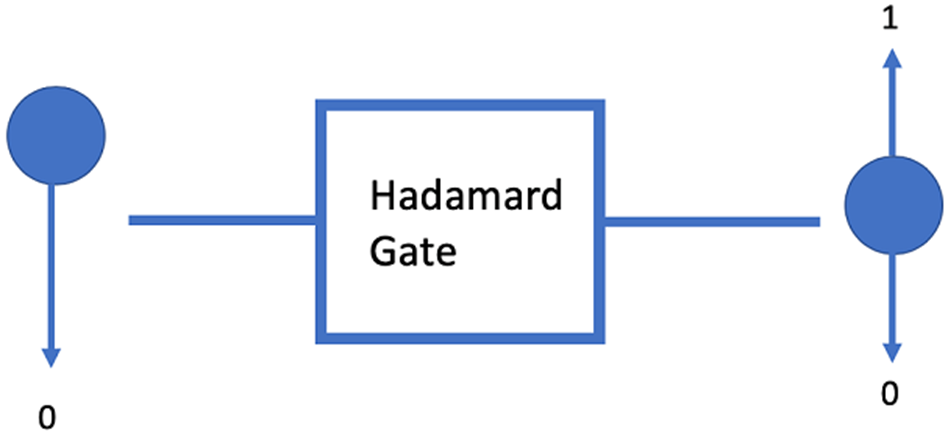
(b) Hadamard Gate (H)
Creates a superposition of |0⟩ and |1⟩.
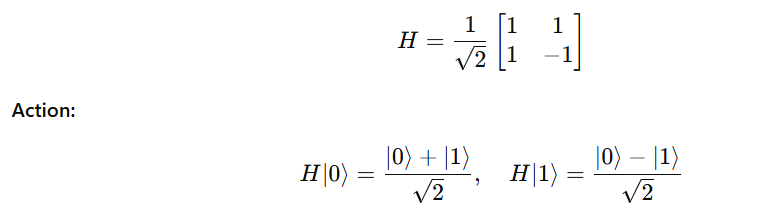
The Hadamard gate is essential for quantum parallelism — it initializes qubits into equal superpositions before running algorithms.
(c) Phase and Rotation Gates

Rotation gates allow continuous control of qubit orientation on the Bloch sphere — critical for analog precision in quantum algorithms.
4.2. Multi-Qubit Gates
These gates act on two or more qubits and are responsible for entanglement, which is key to quantum advantage.
(a) Controlled-NOT (CNOT) Gate

b) Controlled-Z (CZ) Gate
Applies a phase flip if both qubits are |1⟩.
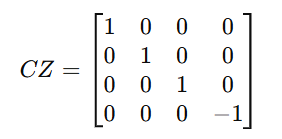
Used in entanglement generation and quantum phase estimation.
(c) Toffoli Gate (CCNOT)
A three-qubit gate that flips the third qubit if the first two are |1⟩.
| Matrix Size: | 8×8 |
| Role: Universal for reversible classical computation and used in error correction.
(d) SWAP Gate
Exchanges the states of two qubits: SWAP∣a,b⟩=∣b,a⟩
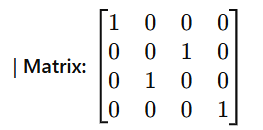
Used to reorder qubits in a circuit or mitigate hardware connectivity limits.
4.3. Composite and Universal Gate Sets
Any quantum computation can be built from a universal gate set, typically:
- {H, S, T, CNOT}
or equivalently - {H, R𝓏(θ), CNOT}
These gates form the foundation for universal quantum computation, meaning they can approximate any unitary operation to arbitrary precision.
5. Quantum Circuit Representation
Quantum gates are visually represented in quantum circuit diagrams, where:
- Horizontal lines = qubits (wires).
- Boxes or symbols = gates.
- Time flows left to right.
Example: Creating an Entangled Bell State
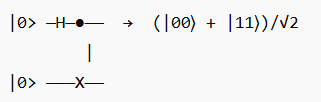
Explanation:
- Apply Hadamard (H) to the first qubit → superposition.
- Apply CNOT using first as control → entangles the two qubits.
6. Measurement after Gates
After applying quantum gates, measurement collapses the superposition into a definite classical outcome.
However, the probability distribution of outcomes depends on the interference of amplitudes produced by the gate operations.
Quantum algorithms exploit this interference to amplify correct answers and suppress incorrect ones, enabling computational speedups.
7. Practical Implementation of Quantum Gates
Quantum gates are physically realized differently depending on the hardware platform:
| Hardware Type | Implementation Method |
|---|---|
| Superconducting Qubits | Microwave pulses controlling Josephson junctions |
| Trapped Ions | Laser pulses tuning electronic transitions |
| Photonic Systems | Beam splitters, phase shifters, and polarizers |
| Spin Qubits | Magnetic or electric field rotations |
| Neutral Atom Qubits | Laser-induced Rydberg excitations |
Each implementation must achieve high-fidelity, low error, and precise timing for accurate computation.
8. Quantum Gate Fidelity and Errors
Real quantum gates are imperfect due to noise and calibration drift.
Gate quality is measured using fidelity — the overlap between the ideal and actual state after gate operation.
Typical values:
- Single-qubit gates: > 99.9% fidelity
- Two-qubit gates: ~98–99% (current leading hardware)
Improving gate fidelity is essential for fault-tolerant quantum computation.
9. Summary
| Property | Quantum Gates |
|---|---|
| Definition | Reversible unitary transformations acting on qubits |
| Mathematical Form | Unitary matrices (U†U = I) |
| Visualization | Rotations and reflections on the Bloch sphere |
| Function | Create, manipulate, and entangle quantum states |
| Types | Single-qubit (H, X, Y, Z, S, T) and Multi-qubit (CNOT, CZ, SWAP, Toffoli) |
| Physical Realization | Laser pulses, microwave control, or optical components |
| Error Metric | Gate fidelity and decoherence time |
| Purpose | Form the logical foundation of all quantum algorithms |
10. Conclusion
Quantum gates are the fundamental operations that bring quantum computation to life.
By rotating qubits, shifting phases, and creating entanglement, they allow quantum computers to perform parallel and interference-based computation impossible for classical systems.
Each gate is a precisely engineered physical interaction, whether achieved through laser pulses, microwave signals, or optical devices.
When combined into quantum circuits, these gates manipulate quantum registers to implement powerful algorithms such as Shor’s, Grover’s, and Quantum Fourier Transform.
In essence:
Quantum gates are rotations instead of logic — they don’t flip switches, they twist probabilities.


